Сравнение квантовой и классической имитации отжига
Contents
Сравнение квантовой и классической имитации отжига#
Автор(ы):
Описание лекции#
В этой лекции рассмотрим каноническую работу Quantum annealing in the transverse Ising model, опубликованную в 1998 году [KN98]. В ней двумя способами численно решается задача о нахождении основного состояния системы взаимодействующих спинов. Первый способ – обычная классическая имитация отжига, второй – имитация квантового отжига. Результаты применения этих подходов анализируются и сравниваются между собой.
Постановка задачи#
Итак, рассматривается одномерная система взаимодействующих спинов, которая описывается гамильтонианом Изинга (полностью аналогичным тому, который был представлен в базовой лекции о модели Изинга):
где \(J_{ij}\) – величины обменного взаимодействия для пар спинов, \(h\) – внешнее поле (оно направлено вдоль оси \(z\) и потому называется продольным – longitudinal). Требуется найти основное состояние гамильтониана \(\hat{H}_{0}\), т.е. его собственное состояние, соответствующее его минимальному собственному значению.
Далее разберем численное решение этой задачи с помощью обычной классической имитации отжига (simulated annealing, SA для краткости) и с помощью квантовой имитации отжига (quantum annealing – QA).
Имитация квантового отжига (QA)#
Как в предыдущей лекции об аннилере D-Wave, добавляем к “целевому” гамильтониану \(\hat{H}_{0}\) (problem Hamiltonian) слагаемое, которое называется tunneling Hamiltonian:
где \(\hat{H}_{tun}(t)\) зависит от времени и отвечает за квантовомеханическое туннелирование между различными собственными состояниями гамильтониана \(\hat{H}_{0}\). Оператор \(\hat{H}_{tun}(t)\) соответствует приложенному внешнему магнитному полю вдоль оси \(x\) (т.е. поперечному, transverse). Когда величина \(\Gamma(t)\) очень велика по сравнению с \(J_{i j}\) и \(h\), собственное состояние гамильтониана \(\hat{H}(t)\), соответствующее его минимальному собственному значению, представляет собой линейную комбинацию всевозможных состояний системы с приблизительно равными амплитудами вероятностей ориентации каждого спина вверх и вниз. Если достаточно медленно уменьшать \(\Gamma(t)\) с очень большой величины до нуля, можно надеяться (в соответствии с адиабатической теоремой), что приведем систему в основное состояние гамильтониана \(\hat{H}_{0}\).
В обсуждаемой статье в качестве примеров рассматриваются три различных закона изменения \(\Gamma(t)\):
\(\Gamma(t) = \frac{c}{\ln(t+1)},\)
\(\Gamma(t) = \frac{c}{\sqrt{t}},\)
\(\Gamma(t) = \frac{c}{t},\)
везде \(t \in (0, +\infty)\) и \(c = \textrm{const}\).
Квантовая динамика системы описывается нестационарным уравнением Шредингера
Это уравнение решается численно (с помощью дискретизации по времени и применения конечно-разностной схемы) для небольшой системы (число спинов \(N=8\)). Измерить близость состояния \(\ket{\psi(t)}\) к основному состоянию \(\ket{g}\) гамильтониана \(\hat{H}_{0}\) можно путем вычисления вероятности
Note
Основное состояние \(\ket{g}\) для небольшого числа спинов можно найти точно, например, путем полного перебора.
Кроме того, можно рассмотреть так называемое квазистатическое приближение. Выберем какое-нибудь значение \(\Gamma = \textrm{const}\) и решим задачу об основном состоянии \(\ket{\psi_{\Gamma}}\) независящего от времени гамильтониана
Следует ожидать, что при очень медленном изменении \(\Gamma(t)\) вероятность
будет близка к \(P_{QA}(t)\) (имеется в виду, что значение \(\Gamma\) соответствует значению \(\Gamma(t)\)). Отличие \(P_{QA}(t)\) от \(P_{QA}^{st}(\Gamma)\) говорит о том, насколько близко состояния системы при динамическом процессе отжига следуют за соответствующими “квазистатическими” состояниями.
Классическая имитация отжига (SA)#
В лекции, посвященной комбинаторной оптимизации, процесс имитации отжига описывался таким образом: выбиралось случайное начальное состояние, затем оно в цикле подвергалось случайной модификации, и новое состояние принималось или отклонялось в соответствии с некоторым критерием. В статье [KN98] принят другой подход к SA. Рассматривается так называемое основное кинетическое уравнение (англ. master equation). Оно описывает классический SA процесс, соответствующий нестационарному уравнению Шредингера (63). В нашем случае это система обыкновенных дифференциальных уравнений для вероятностей нахождения системы в различных состояниях \(i\) в момент времени \(t\):
где \(\mathcal{L}_{i j}\) – вероятность перехода системы из состояния \(j\) в состояние \(i\) (при \(j \neq i\)) в единицу времени. Рассматриваются только элементарные переходы, сопровождающиеся изменением ориентации какого-либо одного спина (остальные спины при данном переходе не меняют ориентацию). Элементы матрицы переходов записываются следующим образом:
Для первого условия правая часть в формуле (65) соответствует распределению Больцмана. Для понимания полезно проанализировать несколько предельных случаев:
если \(E_i < E_j\) и \(\left| E_i - E_j \right| \gg T(t)\), то вероятность перехода \(j \to i\) близка к 1;
если \(E_i > E_j\) и \(E_i - E_j \gg T(t)\), то вероятность перехода \(j \to i\) близка к 0;
если \(\left| E_i - E_j \right| \ll T(t)\), то вероятность перехода \(j \to i\) близка к \(1/2\).
Все случаи соответствуют интуитивным ожиданиям.
Во втором условии в (65) сама сумма (без знака “минус”) равна суммарной вероятности перехода из состояния \(i\) во все остальные состояния. Так что эта сумма должна входить со знаком “минус” в выражение \(\frac{d P_i(t)}{d t}\) для темпа изменения вероятности \(P_i\) нахождения в состоянии \(i\).
Третье условие в (65) означает, что рассматриваем только перевороты одиночных спинов (single-spin flip) в качестве допустимых переходов между состояниями системы.
Зависимость температуры от времени выбирается равной \(\Gamma(t)\):
Близость решения задачи SA к основному состоянию \(\ket{g}\) гамильтониана \(\hat{H}_{0}\) выражается величиной вероятности \(P_g(t)\) найти систему в основном состоянии в момент времени \(t\):
Аналогично квантовому случаю, введем величину \(P_{SA}^{st}(T)\), которая в квазистатическом приближении близка к \(P_{SA}(t)\) (если величина температуры \(T = T(t)\)).
Анализ и сравнение результатов#
В статье обсуждаются численные результаты для \(P_{SA}\) и \(P_{QA}\) для различных конфигураций обменного взаимодействия и различных вариантов зависимости поперечного поля от времени. В всех случаях продольное внешнее поле выбрано постоянным: \(h = 0.1\).
Ферромагнитная модель#
Здесь проводится численный эксперимент для ферромагнитной модели Изинга с \(J_{i j} = \textrm{const}\) для всех пар спинов. Зависимости \(T\) и \(\Gamma\) от времени выбираются такими:
Результаты представлены на Fig. 107.
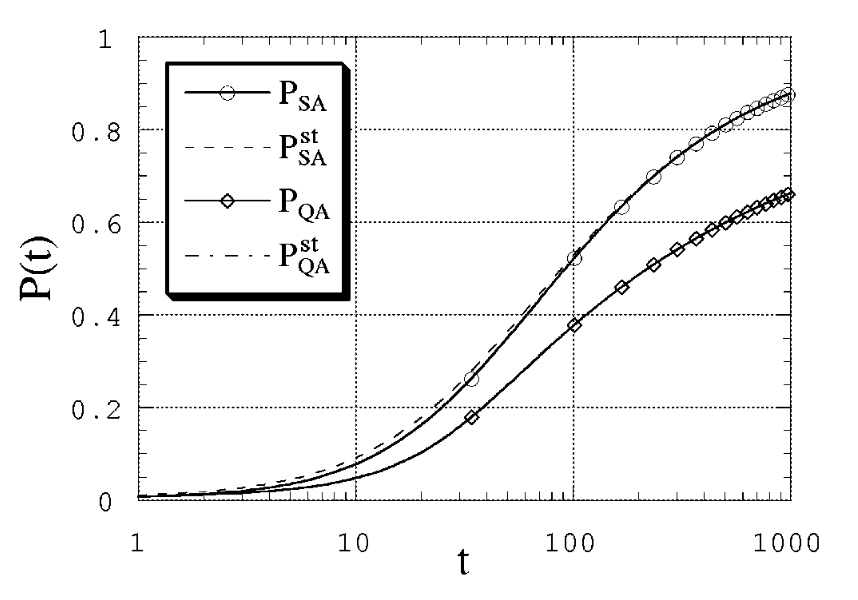
Fig. 107 Зависимости \(P_{SA}(t)\), \(P_{QA}(t)\), \(P_{SA}^{st}(T(t))\) и \(P_{QA}^{st}(\Gamma(t))\) для ферромагнитной модели при \(\Gamma(t) = T(t) = 3 / \ln(t+1)\).#
Видно, что квазистатическое приближение работает очень хорошо, интересующие нас величины в динамическом процессе очень близки к вычисленным в равновесных условиях. Когда расписание отжига имеет вид \(T(t) = c / \ln(t+1)\), гарантируется сходимость \(P_{SA} \to 1\) при подходящем выборе константы \(c\) (в статье [KN98] есть ссылка на соответствующую теорему). Выбор константы \(c = 3\) достаточно произволен, но высокая точность приближенного равенства \(P_{SA}(t) \approx P_{SA}^{st}(T(t))\) свидетельствует о том, что в рассматриваемом случае действительно \(P_{SA} \to 1\) при \(t \to +\infty\).
Для QA нет аналогичного точного утверждения о сходимости \(P_{QA} \to 1\), но численные результаты для данного ферромагнитного случая при \(\Gamma(t) = 3 / \ln(t+1)\) позволяют предположить такую сходимость.
Тот факт, что QA-кривая на Fig. 107 всегда ниже SA-кривой, никакого значения не имеет, потому что в обеих задачах у нас все величины обезразмерены (\(\hbar = 1\) в (63) и единица времени \(\tau = 1\) в (64)) и никакого согласования при обезразмеривании в двух задачах нет.
Если уменьшать поперечное поле и температуру быстрее,
то возникает качественное отличие QA и SA решений, см. Fig. 108.
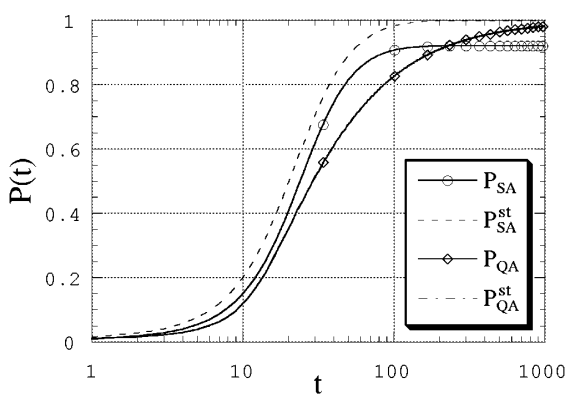
Fig. 108 Вид коэффициентов перекрытия для ферромагнитной модели при \(\Gamma(t) = T(t) = 3 / \sqrt{t}\).#
Видно, что решение квантовомеханической задачи лучше сходится к основному состоянию, чем решение классической задачи. Более того, SA-решение “застревает” в каком-то локальном минимуме с не очень малой вероятностью. На Fig. 109 виден темп приближения \(P_{QA}\) к 1 (на графике двойная логарифмическая шкала). Можно сделать вывод, что \((1 - P_{QA}) \propto 1/t\) в широком диапазоне \(t\).
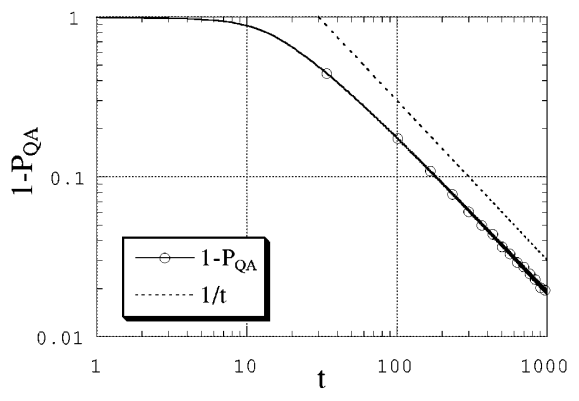
Fig. 109 \((1 - P_{QA}(t))\) для ферромагнитной модели при \(\Gamma(t) = 3 / \sqrt{t}\).#
Если еще быстрее уменьшать поперечное поле и температуру,
то оба решения “застревают” в неосновных состояниях, как видно из Fig. 110.
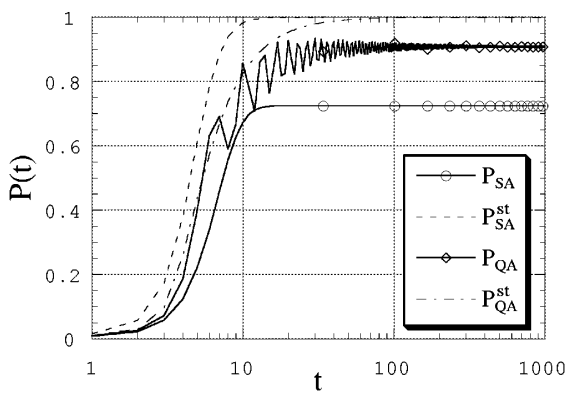
Fig. 110 Вид коэффициентов перекрытия для ферромагнитной модели при \(\Gamma(t) = T(t) = 3 / t\).#
Фрустрированная модель#
Здесь анализируется так называемая фрустрированная (frustrated) система, она изображена на Fig. 111.
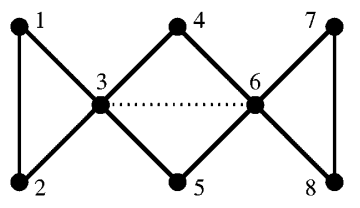
Fig. 111 Фрустрированная система спинов.#
Сплошные линии обозначают ферромагнитное взаимодействие между спинами, пунктирная линия – антиферромагнитное взаимодействие (сила которого по абсолютной величине равна силе ферромагнитного взаимодействия). Если в SA-задаче температура очень велика, то спины 4 и 5 меняют свою ориентацию с очень высокой частотой, так что взаимодействие спинов 3 и 6 посредством спинов 4 и 5 пренебрежимо мало. В этом случае прямое антиферромагнитное взаимодействие между спинами 3 и 6 оказывается доминирующим, поэтому наблюдается отрицательная корреляция между ориентациями спинов 3 и 6 (см. Fig. 112).
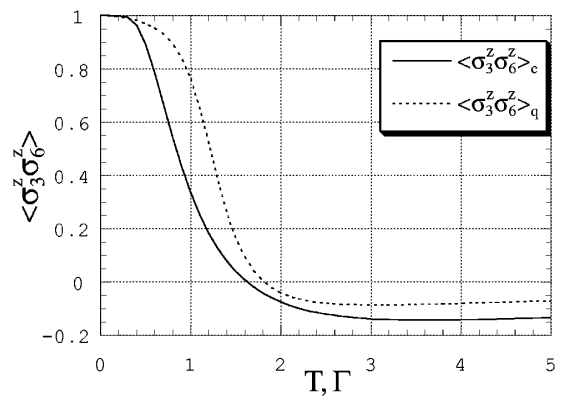
Fig. 112 Величина корреляции спинов 3 и 6. Индекс c означает классическое решение (SA), индекс q означает квантовомеханическое решение (QA).#
С другой стороны, при низкой температуре спины 4 и 5 стремятся принять определенную устойчивую ориентацию. В этом случае эффективное (непрямое) ферромагнитное взаимодействие между спинами 3 и 6 посредством спинов 4 и 5 примерно вдвое сильнее, чем прямое антиферромагнитное взаимодействие. Эти рассуждения подтверждаются положительной величиной корреляции \(\braket{\sigma_3^z \sigma_6^z}_c\) при низких температурах (Fig. 112). Значит, спины 3 и 6 должны поменять взаимную ориентацию при некоторой промежуточной температуре.
Если поперечное поле в QA-задаче играет роль, аналогичную роли температуры в SA-задаче, то следует ожидать схожего поведения величины корреляции \(\braket{\sigma_3^z \sigma_6^z}_q\) при изменении \(\Gamma\). Здесь наблюдаемая \(\braket{\sigma_3^z \sigma_6^z}_q\) вычисляется с использованием основного состояния гамильтониана (62) при заданной \(\Gamma\). Так и есть (см. пунктирную кривую на Fig. 112).
Если использовать расписание отжига
то получаются результаты, изображенные на Fig. 113.
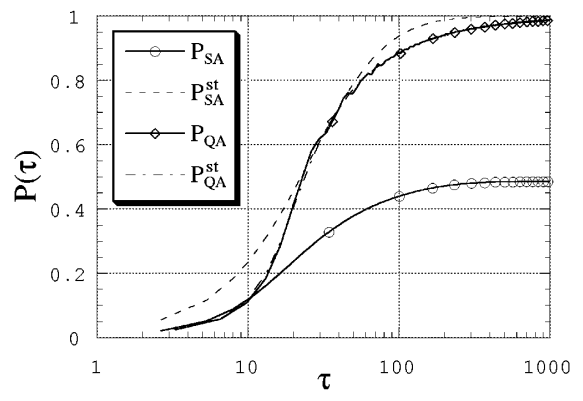
Fig. 113 Вид коэффициентов перекрытия для фрустрированной модели при \(\Gamma(t) = T(t) = 3 / \sqrt{t}\).#
Обезразмеренное время \(\tau = t T_c^2\) для SA-задачи и \(\tau = t \Gamma_c^2\) для QA-задачи. Здесь \(T_c\) и \(\Gamma_c\) – критические величины, при которых \(\braket{\sigma_3^z \sigma_6^z}_c\) и \(\braket{\sigma_3^z \sigma_6^z}_q\) переходят через ноль на графике Fig. 112. Видно, что квантовый отжиг лучше подходит для поиска основного состояния в такой системе.
Модель со случайными взаимодействиями#
Последний рассмотренный пример – это модель спинового стекла, предложенная Шеррингтоном и Киркпатриком [SK75]. Для всех пар спинов есть взаимодействие, сила которого является случайной величиной и семплируется из гауссова распределения с нулевым средним и с дисперсией \(1/N\) (в нашем случае \(N=8\)). На Fig. 114 показан типичный результат для эволюции коэффициентов перекрытия во времени при расписании отжига \(\Gamma(t) = T(t) = 3 / \sqrt{t}\).
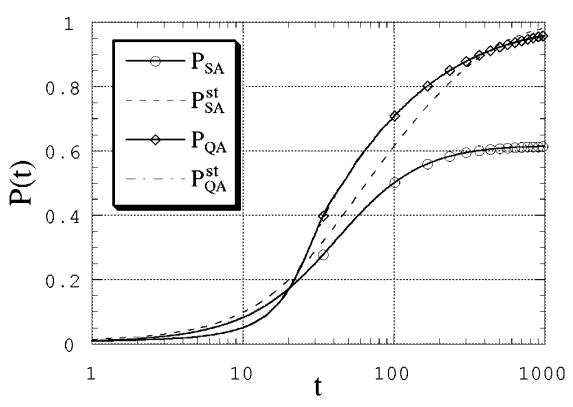
Fig. 114 Вид коэффициентов перекрытия для модели Шеррингтона-Киркпатрика при \(\Gamma(t) = T(t) = 3 / \sqrt{t}\).#
Было проверено несколько реализаций для коэффициентов обменного взаимодействия (семплирование выполнялось из одной и той же функции распределения), результаты оказались качественно близкими. Графики на Fig. 114 подтверждают, что для данной оптимизационной задачи квантовый отжиг подходит лучше, чем классический.
Заключение#
В этой лекции рассказали о канонической работе, в которой для модели Изинга рассмотрены классическая имитация отжига и квантовая имитация отжига, выполнен анализ и сравнение свойств решений в рамках этих двух подходов на нескольких примерах. Выяснилось, что:
при одном и том же расписании отжига квантовый отжиг дает сходимость к основному состоянию с большей вероятностью, чем классический отжиг;
для квантового случая система сходится к основному состоянию при расписании отжига \(\Gamma = c / \sqrt{t}\), но не при более быстром уменьшении поперечного поля;
для ферромагнитной модели при квантовом отжиге вероятность получения основного состояния ведет себя приближенно как \((1 - \frac{\text{const}}{t})\) на больших временах \(t\).
