QUBO-формулировки для линейной регрессии, SVM и метода k-средних
Contents
QUBO-формулировки для линейной регрессии, SVM и метода k-средних#
Автор(ы):
Описание лекции#
Здесь рассмотрим QUBO-формулировки трех задач ML (линейная регрессия, SVM, сбалансированная кластеризация методом k-средних) аналогично тому, как в предыдущей лекции было продемонстрировано сведение к QUBO задач о максимальном разрезе в графе, о коммивояжере и о выделении сообществ в графе. Изложение полностью основывается на статье [DAPN21].
Некоторые обозначения, которые будут использоваться в дальнейшем:
\(\mathbb{R}\) – множество действительных чисел;
\(N\) – количество объектов в обучающем наборе, \(N \in \{1, 2, \dotsc\}\);
\(d\) – количество признаков (features) для объектов в обучающем наборе, \(d \in \{1, 2, \dotsc\}\);
\(X\) – тренировочный набор, содержит по одному объекту в каждой из \(N\) строк, каждая строка содержит \(d\) значений признаков, \(X \in \mathbb{R}^{N \times d}\);
\(Y\) – набор истинных “ответов” (ground truth), соответствующих тренировочным объектам из \(X\) (\(Y \in \mathbb{R}^{N}\) в случае регрессии, \(Y \in \{0,1\}^{N}\) в случае бинарной классификации);
\(\otimes\) – произведение Кронекера (тензорное произведение);
\(\odot\) – произведение Адамара (поэлементное произведение).
Общая формулировка QUBO-задачи, которая используется в статье [DAPN21] и к которой всё сводится, выглядит так:
где \(M\) – натуральное число, \(z\) – бинарный вектор решения, \(A \in \mathbb{R}^{M \times M}\) – QUBO-матрица с действительными элементами, \(b \in \mathbb{R}^{M}\) – QUBO-вектор. Как отмечалось в предыдущей лекции, при \(z_i \in \{0,1\}\) выполняется равенство \(z_i^2 = z_i\), так что линейные члены в (47) можно включить в квадратичные, но этого делать не будем, т.к. для целей этой лекции и для лучшего понимания удобнее сохранить минимизируемую квадратичную форму именно в виде (47).
Линейная регрессия#
В задаче линейной регрессии предполагается, что зависимость истинных ответов от признаков тренировочных объектов приближенно линейная:
где \(y_i^{(pred)}\) – предсказываемое значение, \(y_i\) – истинное значение (из разметки), \(\braket{\cdot, \cdot}\) – скалярное произведение. Удобно сразу избавиться от слагаемого \(b\) (bias), добавив единицу к набору признаков. Тогда bias окажется включенным в веса \(w\), а тренировочный набор будет иметь по \((d+1)\) признаков на объект: \(X \in \mathbb{R}^{N \times (d+1)}\). Требуется найти веса \(w\), при которых квадрат евклидовой нормы невязки минимален:
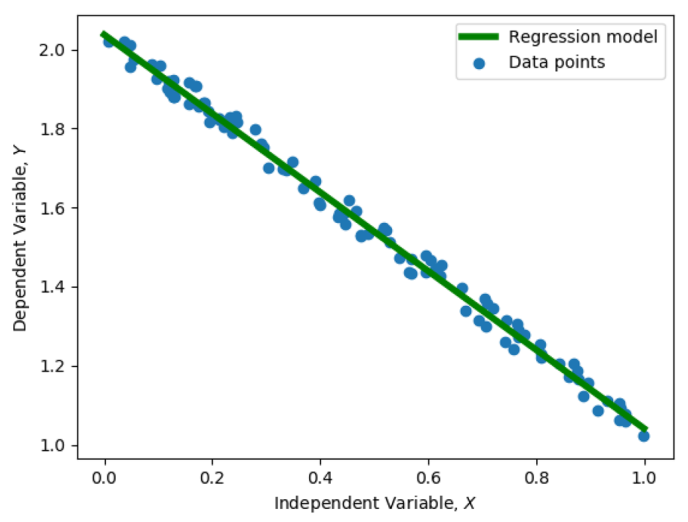
Fig. 94 Иллюстрация к задаче линейной регрессии.#
Известно аналитическое решение задачи (48):
Если \(\left( X^T X \right)^{-1}\) не существует, нужно вычислить псевдообратную матрицу. ВременнАя сложность решения задачи линейной регрессии равна \(\mathcal{O}(N d^2)\), т.к. нужно \(\mathcal{O}(N d^2)\) для вычисления матрицы \(X^T X\) и \(\mathcal{O}(d^3)\) для вычисления обратной к ней (предполагаем, что \(N \gg d\)).
QUBO-формулировка#
Перепишем выражение (48):
Наша цель – найти вектор \(w\), компоненты которого – действительные числа. Но в QUBO-формулировке необходимо представить решение в виде вектора с бинарными компонентами. Как это сделать? Конечно, напрашивается идея использовать бинарное представление действительного числа \(w_i\) (будем отдельно записывать в бинарном виде целую часть, отдельно – дробную). Нужно помнить о том, что знак \(w_i\) может быть как положительным, так и отрицательным. Формат представления придется выбрать фиксированным (т.е. с фиксированной запятой, не с плавающей запятой). Пример:
Бинарные компоненты логично рассматривать как индикаторы наличия или отсутствия соответствующих степеней двойки в бинарном представлении каждого действительного числа. Введем вектор-столбец \(P\), который отвечает за точность представления (Precision vector) и состоит из степеней двойки со знаками:
этот вектор отсортирован по возрастанию элементов. Отводится \(l\) двоичных разрядов для целой части числа, \(m\) разрядов для дробной. \(l\) определяется максимальным по модулю действительным числом, которое хотим представлять; \(m\) определяется желаемой точностью представления. Число элементов вектора \(P\) равно \((m + 1 + l) \cdot2 = K\).
Вводим вектор \(\tilde{w}_i \in \{0,1\}^K\) такой, что
Чтобы не было неоднозначности, нужно договориться о том, что для представления \(w_i > 0\) используем только положительные элементы вектора \(P\), а для \(w_i < 0\) – только отрицательные.
Составляем бинарный вектор \(\tilde{w} \in \{0,1\}^{K(d+1)}\)
и матрицу точности \(\mathcal{P}\) (Precision matrix), которая задает переход к бинарному представлению векторов:
где \(I_{d+1}\) – единичная матрица размера \((d+1)\). Матрица \(\mathcal{P}\) имеет размерность \((d+1) \times K(d+1)\). Исходный вектор весов можно записать как
где знак “=” на самом деле означает приближенное равенство (наше fixed-point представление имеет конечную точность).
Всё готово для того, чтобы переписать исходную задачу (49) в QUBO-формулировке. Подставляем (50) в (49) и получаем
слагаемое \(Y^T Y\) отброшено, т.к. это константа, никак не влияющая на решение задачи оптимизации без ограничений.
Оценка вычислительной сложности#
Для исходной задачи регрессии (48) количество значений в датасете \(X\) равно \(\mathcal{O}(N d)\). Мы ввели \(K\) бинарных переменных для каждого из \((d+1)\) весов. Значит, получилось \(\mathcal{O}(K d)\) переменных в QUBO-формулировке (51). Для решения задачи требуется \(\mathcal{O}(K^2 d^2)\) кубитов (см. [DPP19]), это пространственная сложность в рассматриваемом подходе.
ВременнАя сложность в классической задаче \(\mathcal{O}(N d^2)\). В случае QUBO-задачи для временнОй оценки нужно рассмотреть три части:
Затраты времени для конвертации задачи регрессии в QUBO-формулировку. Здесь получаем \(\mathcal{O}(N K^2 d^2)\) (проверьте это, оценив число умножений, необходимых для вычисления \(\mathcal{P}^T X^T X \mathcal{P}\)).
Время для реализации QUBO-задачи в квантовом “железе”. Здесь потребуется \(\mathcal{O}(K^2 d^2)\), если использовать алгоритм из [DPP19].
Время для выполнения квантового отжига. Существуют теоретические оценки времени для получения точного решения, но более практично рассматривать случай, когда можно просто довольствоваться достаточно высокой вероятностью (скажем, 99%) получения оптимального решения. Для современных квантовых компьютеров D-Wave с ограниченным числом кубитов на практике получается, что время отжига и число повторений можно считать константами.
В итоге полная временнАя сложность решения QUBO-задачи на адиабатическом квантовом компьютере \(\mathcal{O}(N K^2 d^2)\). Может показаться, что это хуже, чем временнАя сложность классического решения, если считать \(K\) переменной. Но величина \(K\) определяется только шириной диапазона числовых значений и желаемой точностью представления, \(K\) не зависит от основных параметров задачи типа \(N\) и \(d\). Поэтому можно считать \(K\) константой. Тогда число требуемых кубитов \(\mathcal{O}(d^2)\), временнАя сложность \(\mathcal{O}(N d^2)\), это эквивалентно классическому случаю.
SVM#
Классический SVM подробно описан в соответствующей лекции. Рассматривается тренировочный набор \(X \in \mathbb{R}^{N \times d}\) и набор истинных меток \(Y \in \{-1, +1\}^{N}\). Нужно решить задачу бинарной классификации, найдя веса \(w \in \mathbb{R}^{d}\) и константу \(b \in \mathbb{R}\), при которых классификатор \(a(x_i) = \text{sign} \left( w^T x_i + b \right)\) допускает как можно меньше ошибок на обучающей выборке.
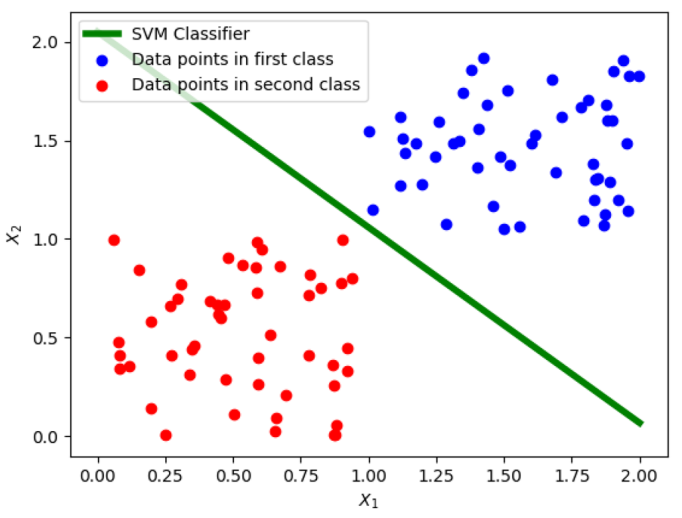
Fig. 95 Иллюстрация к задаче бинарной классификации с помощью SVM.#
Двойственная задача (18) в текущих обозначениях принимает вид
QUBO-формулировка#
Перепишем (52) как задачу минимизации:
Тренировочные объекты \(x_i\), соответствующие \(\lambda_i = 0\), называются периферийными, от них решение
не зависит. Объекты, соответствующие \(\lambda_i > 0\), называются опорными.
Задача минимизации переписывается в виде
где \(1_N\) – вектор, состоящий из \(N\) единиц (аналогичный смысл имеют \(0_N\) и \(C_N\)), \(\lambda \in \mathbb{R}^{N}\).
Как в задаче линейной регрессии, будем представлять каждую \(\lambda_i \in \mathbb{R}\) бинарным вектором \(\tilde{\lambda}_i \in \{0,1\}^K\). Поскольку \(\lambda_i \geq 0\), в precision vector \(P\) нужно включить только положительные значения:
Вектор \(P\) содержит \(m + 1 + l = K\) элементов (здесь \(K\) никак не связано с \(K\) из раздела про линейную регрессию, просто было решено не вводить новое обозначение для длины нового вектора \(P\)). При подходящем выборе \(m\) и \(l\) достаточно точно выполняется равенство
Выполняем конкатенацию всех \(\tilde{\lambda}_{i k}\) по вертикали
и вводим матрицу \(\mathcal{P}\) (precision matrix)
таким образом, что (приближенно)
Подставляя из этого выражения \(\lambda\) в (54), получаем:
Остается избавиться от ограничения в виде равенства в (56). Как обычно делается в таких случаях, вместо ограничения вводим соответствующий штраф за его нарушение:
где \(\gamma\) – достаточно большая константа, hp означает hyperplane (гиперплоскость).
Добавляем \(Penalty^{(hp)}\) к \(\mathcal{L}_{neg}(\tilde{\lambda})\) и получаем итоговую QUBO-формулировку:
Оценка вычислительной сложности#
Задача (54) содержит \(\mathcal{O}(N d)\) значений в данных и \(\mathcal{O}(N)\) параметров (\(\lambda\)). QUBO-формулировка (57) содержит то же количество данных, а число параметров в \(K\) раз больше, т.е. \(\mathcal{O}(K N)\). Значит, потребуется \(\mathcal{O}(N^2 K^2)\) кубитов.
ВременнАя сложность классического SVM в типичных реализациях (например, LIBSVM) равна \(\mathcal{O}(N^3)\). Для оценки временнОй сложности QUBO рассматриваем три составляющие (как в задаче линейной регрессии):
Затраты времени для конвертации в QUBO-формулировку. Из (53) и (55) следует, что оценка времени \(\mathcal{O}(N^2 K^2)\).
Для реализации QUBO-задачи в квантовом “железе” потребуется \(\mathcal{O}(N^2 K^2)\).
Время для выполнения квантового отжига и число повторений можно считать константами (см. комментарии к тому же пункту в обсуждении линейной регрессии).
В итоге временнАя сложность \(\mathcal{O}(N^2 K^2)\). \(K\) можно считать константой, т.к. она зависит только от диапазона и желаемой точности представления \(\lambda\) и не зависит от параметров самой задачи классификации. Тогда получается временная сложность \(\mathcal{O}(N^2)\), что гораздо лучше оценки \(\mathcal{O}(N^3)\) в классическом случае.
Сбалансированная кластеризация методом k-средних#
Кластеризация методом k-средних – ML-задача обучения без учителя (unsupervised). Требуется распределить тренировочные объекты по \(k\) кластерам так, чтобы суммарное отклонение тренировочных объектов, принадлежащих кластерам, от центроидов (центров масс) соответствующих кластеров было минимальным. Сбалансированная кластеризация методом k-средних – частный случай, в котором каждый кластер содержит примерно одно и то же количество объектов \(N/k\), как показано на Fig. 96.
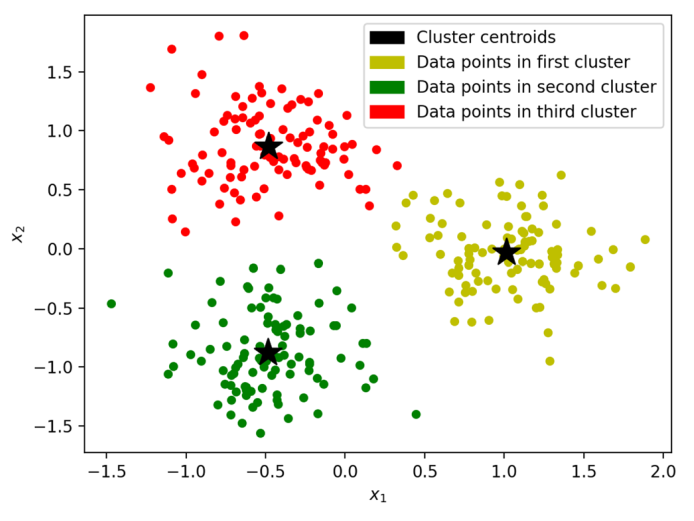
Fig. 96 Иллюстрация к задаче сбалансированной кластеризации методом k-средних.#
Нужно распределить \(N\) объектов из тренировочного набора \(X \in \mathbb{R}^{N \times d}\) по \(k\) кластерам \(\Phi = \{\phi_1, \dotsc, \phi_k\}\). Пусть \(\mu_i\) – центроид кластера \(\phi_i\). В общем случае задача кластеризации методом k-средних формулируется так:
Если размеры \(|\phi_i|\) всех кластеров одинаковые, то формулировка переписывается так:
В прикладных задачах кластеризации размеры кластеров только приближенно равны друг другу, поэтому решение задачи (59) не является точным решением задачи (58). Для решения задачи кластеризации методом k-средних можно использовать, например, алгоритм Ллойда. Существует модификация алгоритма Ллойда для случая сбалансированной кластеризации.
QUBO-формулировка#
Вводим матрицу \(D \in \mathbb{R}^{N \times N}\), элементы которой равны квадратам попарных расстояний между тренировочными объектами:
Также вводим бинарную матрицу \(\tilde{W} \in \{0,1\}^{N \times k}\), каждый элемент которой \(\tilde{w}_{ij} = 1\) в том и только в том случае, когда объект \(x_i\) принадлежит кластеру \(\phi_j\). Очевидно, есть два ограничения на \(\tilde{W}\):
Поскольку мы предполагаем, что все кластеры содержат примерно одно и тоже количество объектов, каждый столбец \(\tilde{W}\) должен содержать примерно \(N/k\) единиц.
Каждый объект принадлежит ровно одному кластеру, поэтому каждая строка \(\tilde{W}\) должна содержать ровно одну единицу.
Для получения QUBO-формулировки задачи нам потребуется избавиться от этих ограничений. Для этого, как обычно, введем в минимизируемую квадратичную форму штрафы за нарушение ограничений. Вернемся к этому через пару абзацев.
Используя \(D\) и \(\tilde{W}\), мы можем переписать внутреннюю сумму в (59) в виде
где \(\tilde{w}_{j}^{'}\) – столбец номер j в \(\tilde{W}\). Чтобы переписать в бинарных переменных полную (двойную) сумму в (59), составим вектор-столбец из всех \(N k\) элементов матрицы \(\tilde{W}\):
При условии, что ограничения на \(\tilde{w}\) выполнены, запишем задачу (59) в эквивалентном виде
Теперь разбираемся с ограничениями на \(\tilde{w}\).
Во-первых, каждый столбец \(\tilde{W}\) должен содержать примерно \(N/k\) единиц. Введем штраф, непосредственно отражающий это требование:
где \(\alpha\) – достаточно большая константа. Раскрыв скобки в предыдущем выражении, можно убедиться, что
Сумма всех штрафов для столбцов равна
Во-вторых, каждая строка \(\tilde{W}\) должна содержать ровно одну единицу. Соответствующий штраф
где \(\beta\) – достаточно большая константа. Раскрыв скобки в предыдущем выражении, получаем
Чтобы найти сумму \(Penalty^{(row)} = \sum_i Penalty_{i}^{(row)}\), преобразуем бинарный вектор \(\tilde{w}\) в другой бинарный вектор \(\tilde{v}\), получающийся из \(\tilde{w}\) определенной перестановкой элементов:
Переход от \(\tilde{w}\) к \(\tilde{v}\) можно представить как линейное преобразование
с некоторой матрицей \(Q \in \{0,1\}^{Nk \times Nk}\) (матрица \(Q\) в свою очередь получается из единичной матрицы \(I_{Nk}\) определенной перестановкой элементов).
Сумма штрафов для строк равна
Соберем вместе квадратичную форму (60) (записанную без учета ограничений) и штрафы \(Penalty^{(col)}\), \(Penalty^{(row)}\) в одно финальное выражение, которое и является QUBO-формулировкой задачи о сбалансированной кластеризации методом k-средних:
Оценка вычислительной сложности#
Задача (59) содержит \(\mathcal{O}(N d)\) значений в данных и \(\mathcal{O}(N)\) переменных. В QUBO-формулировке вводим по \(k\) бинарных переменных для каждой исходной. Получается \(\mathcal{O}(N k)\) переменных, а значит, требуется \(\mathcal{O}(N^2 k^2)\) кубитов.
Известно, что классический алгоритм сбалансированной кластеризации методом k-средних сходится за время \(\mathcal{O}(N^{3.5} k^{3.5})\) в худшем случае (см. ссылки в статье [DAPN21]). Для оценки временнОй сложности QUBO рассматриваем три составляющие:
Затраты времени для конвертации в QUBO-формулировку. В выражении (61) по вычислительной сложности доминирует слагаемое, содержащее \(I_k \otimes D\). Соответствующая вычислительная сложность \(\mathcal{O}(N^2 k d)\).
Для реализации QUBO-задачи в квантовом “железе” потребуется \(\mathcal{O}(N^2 k^2)\).
Время для выполнения квантового отжига и число повторений можно считать константами (см. комментарии к тому же пункту в обсуждении линейной регрессии).
В итоге получаем полную вычислительную сложность \(\mathcal{O}(N^2 k (d+k))\). Это лучше, чем результат классического алгоритма в худшем случае. Но количество итераций в классическом алгоритме сильно зависит от “удачности” начального приближения для центроидов кластеров. Классический алгоритм может оказаться и быстрее квантового.
Заключение#
В этой лекции были рассмотрены три важные задачи машинного обучения, которые можно переформулировать в виде QUBO (Quadratic Unconstrained Binary Optimization) для решения на квантовом аннилере путем сведения к задаче нахождения основного состояния квантовой системы. Общий подход заключается в том, что минимизируемый в классической формулировке функционал переписывается в виде квадратичной формы относительно бинарных переменных, а вместо условий-ограничений в финальную квадратичную форму QUBO-задачи вводятся штрафы за нарушение этих ограничений. Есть надежда на то, что при некотором количестве кубитов квантовые алгоритмы будут иметь преимущество перед классическими по времени выполнения.