Квантовое сверхплотное кодирование
Квантовое сверхплотное кодирование#
Автор(ы):
Сверхплотное кодирование (Superdense coding) – простое, но при этом довольно неожиданное приложение квантовой механики. Оно комбинирует определенным нетривиальным образом большинство основных идей этой физической теории, и потому является отличным примером решения задач обработки информации с помощью квантовой механики.
В задаче о сверхплотном кодировании рассматриваются два действующих лица – Алиса и Боб. Они могут находиться, вообще говоря, далеко друг от друга. Цель – передать некоторое количество классической информации от Алисы к Бобу. Пусть у Алисы есть два классических бита информации, которые она хочет передать Бобу, но Алисе разрешено переслать Бобу только один кубит. Достижима ли эта цель?
Задача о сверхплотном кодировании в некотором смысле противоположна задаче о квантовой телепортации:
квантовая телепортация |
сверхплотное кодирование |
|---|---|
передача одного кубита с помощью двух классических бит |
передача двух классических бит с помощью одного кубита |
Ответ на вопрос выше – утвердительный. Пусть изначально у Алисы и Боба есть пара кубитов в запутанном состоянии
(это первое состояние Белла (11) из четырёх, перечисленных в предыдущей лекции о квантовой телепортации). Вначале первый кубит находится у Алисы, второй – у Боба. Обратите внимание, что для приготовления состояния \( \ket{\psi} \) Алисе не требовалось присылать Бобу никаких кубитов. Некое третье действующее лицо могло приготовить запутанное состояние \( \ket{\psi} \) заранее и переслать первый кубит Алисе, второй – Бобу.
Оказывается, Алиса может передать два бита классической информации Бобу, отправив ему свой кубит. Для этого Алиса выполняет следующую процедуру:
Если Алиса хочет передать Бобу битовую строку “00”, она ничего не делает со своим кубитом.
Если Алиса хочет передать битовую строку “01”, она применяет оператор \(X\) (гейт \(NOT\)) к своему кубиту.
Если Алиса хочет передать битовую строку “10”, она применяет оператор \(Z\) к своему кубиту.
Если Алиса хочет передать битовую строку “11”, она применяет оператор \(ZX = iY\) к своему кубиту.
В результате получаются состояния двухкубитной системы справа от стрелок в следующих формулах (проверьте это!):
т.е. как раз четыре состояния Белла. Они образуют ортонормированный базис в пространстве состояний двухкубитной системы (убедитесь в этом самостоятельно). Следовательно, эти четыре состояния можно различить подходящим измерением для двухкубитной системы. Если Алиса отправит свой кубит Бобу, то Боб после измерения двухкубитной системы в базисе Белла сможет определить, которую из четырех возможных битовых строк Алиса хотела отправить.
Бобу для декодирования удобно было бы применить некий двухкубитный унитарный оператор, отображающий базис Белла в вычислительный базис (чтобы в итоге выполнить измерение в вычислительном базисе). Для этого можно применить оператор \(CNOT\) (первый кубит – контрольный) и затем оператор Адамара \(H\) для первого кубита, как показано в пунктирном блоке в нижнем правом углу на общей схеме:
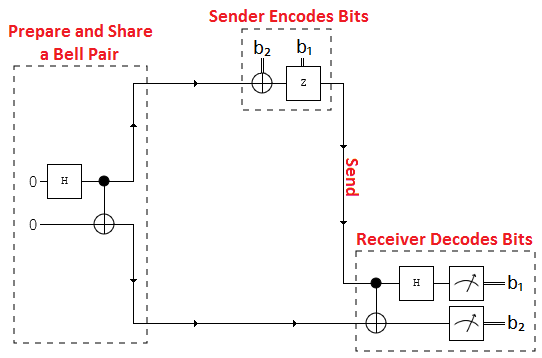
Fig. 31 Общая схема для решения задачи о сверхплотном кодировании#
В качестве упражнения проверьте самостоятельно, что произведение операторов \((H \otimes I) CNOT\) действительно переводит базис \(\left\{ \ket{\beta_{00}}, \ket{\beta_{01}}, \ket{\beta_{10}}, \ket{\beta_{11}} \right\}\) в базис \( \left\{ \ket{00 }, \ket{01}, \ket{10}, \ket{11} \right\} \).
Приведем код на qiskit.
from qiskit import QuantumCircuit
qc = QuantumCircuit(2)
# готовим состояние beta_{00} из стартового состояния |00>:
qc.h(0)
qc.cx(0, 1)
# визуальный разделитель при отрисовке схемы:
qc.barrier()
# выбираем какое-либо сообщение из набора в assert-выражении ниже:
message = '10'
assert message in ('00', '01', '10', '11')
# Алиса выполняет кодирование сообщения:
if message[1] == "1":
qc.x(0)
if message[0] == "1":
qc.z(0)
qc.barrier()
# Боб декодирует сообщение:
qc.cx(0, 1)
qc.h(0)
# Боб измеряет двухкубитную систему целиком (в вычислительном базисе):
qc.measure_all()
qc.draw()
┌───┐ ░ ┌───┐ ░ ┌───┐ ░ ┌─┐
q_0: ┤ H ├──■───░─┤ Z ├─░───■──┤ H ├─░─┤M├───
└───┘┌─┴─┐ ░ └───┘ ░ ┌─┴─┐└───┘ ░ └╥┘┌─┐
q_1: ─────┤ X ├─░───────░─┤ X ├──────░──╫─┤M├
└───┘ ░ ░ └───┘ ░ ║ └╥┘
meas: 2/═══════════════════════════════════╩══╩═
0 1 Запускаем схему на симуляторе:
from qiskit import Aer
aer_sim = Aer.get_backend('aer_simulator')
result = aer_sim.run(qc).result()
counts = result.get_counts(qc)
print(
f"message was '{message}' -> the measurement result is {counts}"
" (<- NOTE: the keys are little-endian!)"
)
message was '10' -> the measurement result is {'01': 1024} (<- NOTE: the keys are little-endian!)
RTFM!
Обратите внимание на документацию к qiskit.result.Result.get_counts! Ключи возвращаемого словаря – это битовые строки в little-endian формате, т.е. кубит с индексом [0] находится справа в битовой строке.
Инициализируем переменную message каждым из четырех значений и получаем следующие результаты:
message was '00' -> the measurement result is {'00': 1024}
message was '01' -> the measurement result is {'10': 1024}
message was '10' -> the measurement result is {'01': 1024}
message was '11' -> the measurement result is {'11': 1024}
Резюмируем. Алиса, взаимодействуя только с одним кубитом, смогла передать два классических бита информации Бобу. Конечно, в процедуре участвовало два кубита, но Алисе не требовалось взаимодействовать со вторым кубитом. Если бы Алиса пересылала Бобу один классический бит вместо одного кубита, то передать таким способом два классических бита было бы невозможно, разумеется.
Существуют более впечатляющие, чем сверхплотное кодирование, примеры применения квантовой механики к задачам обработки информации. Но на примере сверхплотного кодирования виден важнейший принцип – информация физична. Нетривиальные физические теории вроде квантовой механики могут привести к неожиданным новым возможностям в обработке информации.
Напоследок рассмотрим вопрос безопасности коммуникации. Допустим, некий третий субъект (пусть с именем Ева) хочет “подслушать” сообщение, передаваемое Бобу. Ева перехватывает кубит, отправленный Алисой, и может попытаться извлечь какую-либо полезную информацию, выполнив какое-либо измерение над кубитом Алисы. Пусть Ева использует положительно-определенный оператор \(E\) для первого кубита и вычисляет величину \(\braket{\xi | E \otimes I | \xi}\), где \(\ket{\xi}\) – одно из состояний \(\left\{ \ket{\beta_{00}}, \ket{\beta_{01}}, \ket{\beta_{10}}, \ket{\beta_{11}} \right\}\). Кубит Боба (второй кубит) Еве недоступен, поэтому мы поставили единичный оператор на второе место в составном операторе. Любое возможное состояние \(\ket{\xi}\) можно записать в виде
где \(\ket{\phi_1}, \ket{\phi_2}\) – двухкубитные состояния, соответствующие вычислительному базису (см. формулы для \(\ket{\beta_{ij}}\) выше). Например, \(\ket{\phi_1} = \ket{01}, \ket{\phi_2} = -\ket{10}\) для случая \(\ket{\xi} = \ket{\beta_{11}}\) и т.д.
В каждом из четырех возможных случаев \(\braket{\phi_1 | E \otimes I | \phi_2} = \braket{\phi_2 | E \otimes I | \phi_1} = 0\), потому что второй кубит имеет противоположные значения в \(\ket{\phi_1}\) и \(\ket{\phi_2}\). Вычислив \(\braket{\phi_i | E \otimes I | \phi_i}\) для \(i = 1, 2\) (первые два слагаемых в правой части), легко убедиться, что
во всех случаях. Таким образом, Ева всегда будет получать один и тот же результат своего измерения, не зависящий от сообщения, которое Алиса пыталась передать Бобу. Ева не сможет получить никакой полезной информации о сообщении от Алисы, перехватив её кубит.
Лекция и реализация процедуры сверхплотного кодирования в Qiskit
