Преобразование Жордана-Вигнера
Contents
Преобразование Жордана-Вигнера#
Автор(ы):
Описание лекции#
В этой лекции мы узнаем как реально существующей системе (например, электронам на решетке) сопоставить систему состоящую из спинов (кубитов), для того чтобы просимулировать ее на квантовом компьютере. Для этого мы сначала изучим альтернативный, зачастую более удобный подход к описанию многочастичных квантовых систем, который называется “вторичное квантование”.
Введение#
Для того чтобы просимулировать квантовую систему на квантовом же компьютере (например, посчитать энергию основного состояния какого-нибудь атома), нам необходимо закодировать состояние системы и действующие на нее операторы: найти соответствие между состояниями системы и состояниями нашего компьютера (т.е., кубитов).
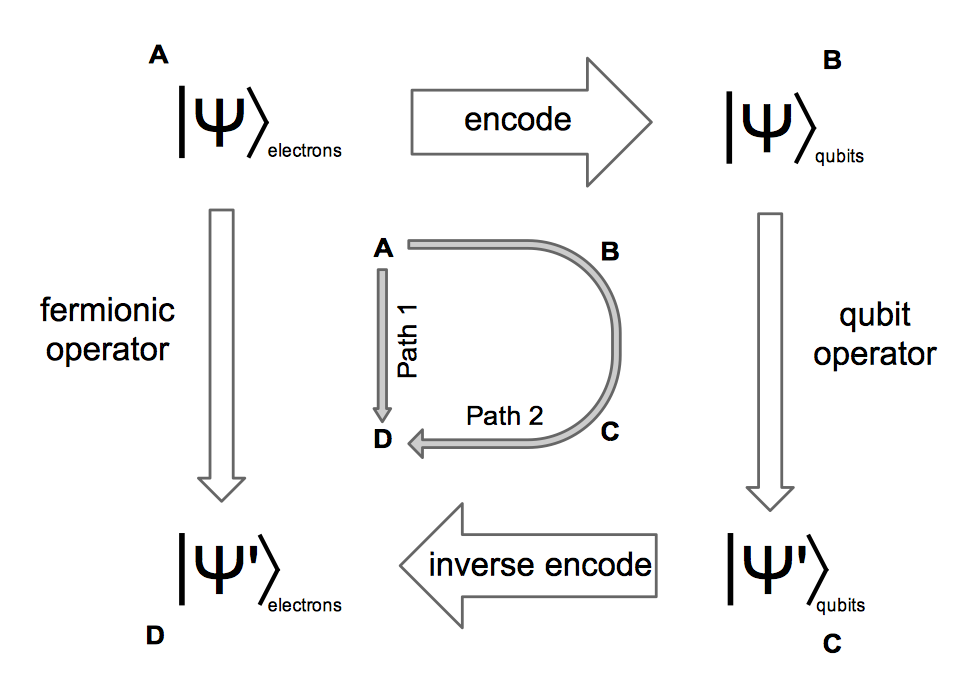
Fig. 97 Общая схема симуляции квантовой системы на квантовом компьютере (взято из [SRL12]).#
Спины, фермионы и бозоны#
Как мы помним из лекции по квантовой химии, квантовые частицы могут быть либо бозонами, либо фермионами. Одно из различий между ними состоит в том, что при перестановки двух бозонов волновая функция не меняется, а при перестановке двух фермионов – меняет знак. Эта классификация следует из того, что квантовые частицы неотличимы.
Несмотря на то, что наши кубиты состоят из каких-то частиц (бозонов или фермионов), обычно они отличимы (например, зафиксированы на своих позициях) и, следовательно, не являются ни бозонами, ни фермионами. Так как мы используем два состояния кубита (\(| 0 \rangle\) и \(| 1 \rangle\)), каждый кубит может быть описан как система со спином 1/2.
Вторичное квантование#
В квантовой механике мы можем описать состояние нескольких частиц как тензорное произведение состояний каждой из частиц. Например, если у нас есть две частицы, и их квантовое состояние описывается положением частицы в пространстве, \(r_i\), мы можем записать состояние частиц как
У этого подхода есть два главных недостатка – во первых, работать с системами в которых разное количество частиц, или где это количество может меняться, не очень удобно. Во-вторых, не учитывается неразличимость квантовых частиц.
Обе эти проблемы решаются вторичным квантованием, где вместо использования состояния каждой частицы мы описываем систему количеством частиц в каждом из возможных состояний. Так как частицы неразличимы, такое описание достаточно для полного описания системы. Вместо Гильбертова пространства фиксированной размерности наши состояния теперь являются элементами пространства Фока (суммы Гильбертовых пространств для всех возможных значений количества частиц). Основное состояние, или вакуум, теперь это состояние с 0 частиц.
Note
Несмотря на название, мы не квантуем систему повторно, а просто избавляемся от избыточности в описании.
Мы так же можем определить операторы, которые добавляют или убирают частицу в определенном состоянии из системы. На языке первой квантизации:
Note
До сих пор операторы которые мы видели действовали из гильбертова пространства с определенным количеством частиц в него самого. Оператор создания действует из гильбертова пространства с \(n\) частиц в гильбертово пространства с \(n+1\) частиц (оба этих пространства являются частью пространства Фока).
Тут \(b^\dagger_\alpha\) называется оператором создания (creation), а \(b_\alpha\) – уничтожения (annihilation). Заметим, что эти операторы не эрмитовы, т.е., \(b^\dagger_\alpha \neq b_\alpha\). Нормализация операторов выбрана таким образом, что собственные значения (эрмитова) оператора \(b^\dagger_\alpha b_\alpha\) – количество частиц в состоянии \(\alpha\).
Note
Наблюдаемые величины соответсвуют эрмитовым операторам, следовательно \(b_\alpha\) не соответсвует никакой наблюдаемой величине. В частности, такой член сам по себе не может быть частью гамильтониана (но может быть частью эрмитова члена, например \(b_\alpha+b^\dagger_\alpha\).
Если в системе нет ни одной частицы в состоянии \(\alpha\), то оператор уничтожения уничтожает состояние:
\(0\) тут это нулевой вектор, в отличии от \(| 0 \rangle\), вакуума. Так как \(0\) это не физическое состояние (например, если бы мы захотели измерить какую-нибудь величину \(X\), то вероятность найти систему в любом собственном состоянии \(| x \rangle\) будет равно нулю), мы можем интерпретировать это как тот факт, что нельзя уничтожить частицу которой нет.
Note
Хотя стандартная конвенция говорит о том, что векторы состояния нормализованы (\(\langle \psi | \psi \rangle = 1\)), после применения оператора (эрмитова или нет) мы не обязаны получить нормализованное состяние. Можно считать что после каждого применения оператора мы нормализуем состояние, либо, чуть более математически, что мы рассматриваем проективное гильбертово пространство, которое задается классом эквивалентности \(v \sim kv\) для комплексного числа \(k \in \mathbb{C}\) и любого вектора \(v \in \mathcal{H}\) т.е. все параллельные векторы эквивалентны.
В зависимости от типа частиц, операторы создания и уничтожения подчиняются определенным отношениям. В случае бозонов, разные операторы коммутируют:
В случае фермионов, операторы антикоммутируют:
В частности,
и, следовательно, в системе не может быть больше одного фермиона в одном состоянии (в соответствии с принципом запрета Паули). Из этого так же следует что \(c_j^2=0\), так как независимо от состояния системы, после первого оператора в ней не останется фермиона который можно было бы уничтожить.
Переход от спинов к фермионам#
Пронумеруем возможные состояния частиц индексом \(i\): например, это могут быть электроны в состояниях, отвечающих гауссианам из STO-3g или находящиеся в разных узлах цепочки атомов. Мы можем попробовать сопоставить спину фермион: если спин с индексом \(i\) направлен вниз то фермион c индексом \(i\) существует, а если спин направлен вверх – то фермион не существует (количество фермионов с определенным индексом может быть только \(1\) или \(0\)). Другими словами, используя оператор количества частиц \(\hat{n}_i = c^\dagger_i c_i\), где \(c^\dagger_i\) и \(c_i\) это операторы создания и уничтожения соответственно, мы хотели бы сопоставить
Тогда лестничные (ladder) операторы \(\sigma^- = (\hat{\sigma}_i^x-i\hat{\sigma}_i^y)/2 = \begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix}\) и \(\sigma^+= (\hat{\sigma}_i^x+i\hat{\sigma}_i^y)/2 = \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}\), соответствуют операторам создания и уничтожения.
Note
Заметим что оператор \(\sigma^-\) переводит состояние “спин вверх” в состоянии “спин вниз”, а состяние “спин вниз” уничтожает. \(\sigma^+\) переводит состояние “спин вниз” в состоянии “спин вверх” (а состяние “спин вверх” уничтожает). Оба этих оператора неэрмитовы.
Действительно, в одном состоянии (если индексы двух операторов равны) эти операторы выполняют фермионное антикоммутационное отношение
К сожалению, на разных узлах эти операторы коммутируют, а не антикоммутируют. Чтобы это исправить, мы “прикрепляем” к каждому фермиону “нить” (string):
Oператор \(\prod_{j_i} (1-2c^\dagger_j c_j)\) равен \(\pm 1\) в зависимости от четности количества фермионов слева от узла \(i\).
Заметим, что \(c_k\) антикоммутирует с \((1-2c^\dagger_k c_k)\):
и, следовательно, с нитью \(\prod_{j_i} (1-2c^\dagger_j c_j) \) (интуитивно, если сначала разрушить фермион, то четность изменится).
Пусть, без ограничения общности, \(\ell>k\):
Если мы перенесем \(c_k\) вправо, то выражение умножится на \(-1\) дважды (один раз из-за изменения четности \(\ell\)-нити, и один раз из-за обмена с \(c^\dagger_\ell\)). В то же время, \(i\)-нить коммутирует со всем, поэтому ее мы можем перенести вправо без изменений:
как и требовалось. Мы так же можем записать обратное отношение:
Проверка антикоммутаторов оставляется читателю в качестве упражнения.
Таким образом мы установили соответствие между фермионной и спиновой системами, но операторы в обоих случаях очень нелокальны. В частности, один фермионный оператор соответствует произведению \(\mathcal{O}(N)\) спиновых операторов (и наоборот).
Note
Существуют и другие способы сопоставления фермионной и спиновой систем, например, Bravyi–Kitaev transform [BK02]. Также существует способ сопоставить бозоны и фермионы – бозонизация [VDS98].
Пример. Модель Хаббарда#
Одной из важных моделей в физике твёрдого тела является модель Хаббарда, описывающая взаимодействие электронов на решетке. В соответствии с принципом Паули, на каждом узле может быть максимум два электрона (один со спином вверх и один со спином вниз).
Гамильтониан модели Хаббарда состоит из двух членов. Первый, кинетический, описывает движение электрона по решетке:
где \(\langle i,j \rangle\) означает что \(i\) и \(j\) индексы соседних узлов решетки, \(\sigma\) обозначает спин электрона, а \(h.c.\) (hermtian conjugate) обозначает слагаемое, эрмитово сопряжённое написанному.
Оператор \(c^\dagger_{i, \sigma}c_{j, \sigma}\) уничтожает электрон на узле \(j\) и создает электрон с таким же спином на узле \(i\), то есть, фактически, перемещает электрон с узла \(j\) на узел \(i\).
Note
Эрмитово сопряжённый оператор \(\left(c^\dagger_{i, \sigma}c_{j, \sigma}\right)^\dagger = c^\dagger_{j, \sigma}c_{i, \sigma}\) перемещает электрон с узла \(i\) на узел \(j\).
Так как этот член квадратичный, мы можем точно решить гамильтониан содержащий только его.
Второй член содержит отталкивающее взаимодействие двух электронов на одном узле, соответствующее отталкиванию двух зарядов:
Полный гамильтониан
Для того чтобы описать соответствующий спиновый Гамильтониан, каждому узлу мы сопоставим два кубита (один для каждого фермиона). Для простоты, рассмотрим одномерную цепочку:
Следовательно, кинетическая часть равна
Заметим, что хоть каждый оператор создания/уничтожения сильно не локален, в их произведении большая часть произведения отменяется (так как \(\left( \sigma^z_j \right)^2=1\):
Второй член дает нам (используя \( \hat{\sigma}_i^z = 1 - 2\hat{n}_i \))
Таким образом, мы получили спиновый гамильтониан:
