PennyLane
Contents
PennyLane#
Автор(ы):
PennyLane – библиотека Python для квантового машинного обучения, которую можно использовать для обычных квантовых вычислений. Программы, написанные на PennyLane, можно запускать, используя в качестве бэкенда настоящие квантовые компьютеры от IBM Q, Xanadu, Rigetti и другие, либо квантовые симуляторы.
Кубиты в PennyLane называются по-особому – wires (от англ. wires – провода). Такое название, скорее всего, связано с тем, что на квантовых схемах кубиты изображаются в виде продольных линий.
Последовательность квантовых операций называется квантовой функцией. Такая функция может принимать в качестве аргументов только хэшируемые объекты. В качестве возвращаемого значения выступают величины, связанные с результатами измерения: ожидаемое значение, вероятности состояний или результаты сэмплирования.
Квантовая функция существует не сама по себе, она запускается на определенном устройстве – симуляторе либо настоящем квантовом компьютере. Такое устройство в PennyLane называется device.
QNode#
Квантовые вычисления при использовании PennyLane раскладываются на отдельные узлы, которые называются QNode. Для их создания используются квантовые функции совместно с device.
Создавать объекты квантовых узлов можно двумя способами: явно либо с помощью декоратора QNode.
Рассмотрим первый способ – явное создание узла.
import pennylane as qml
from pennylane import numpy as np
qml.drawer.use_style("default")
dev = qml.device("default.qubit", shots=1000, wires=2)
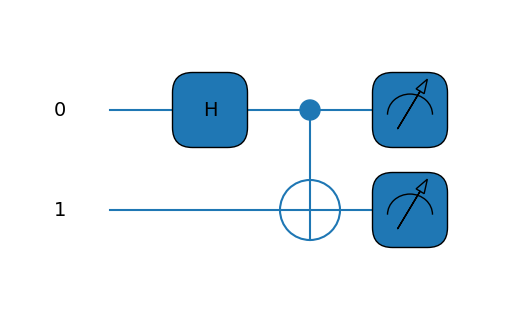
def make_entanglement():
qml.Hadamard(wires=0)
qml.CNOT(wires=[0, 1])
return qml.probs(wires=[0, 1])
circuit = qml.QNode(make_entanglement, dev)
circuit()
/home/runner/work/qmlcourse/qmlcourse/.venv/lib/python3.8/site-packages/_distutils_hack/__init__.py:33: UserWarning: Setuptools is replacing distutils.
warnings.warn("Setuptools is replacing distutils.")
tensor([0.494, 0. , 0. , 0.506], requires_grad=True)
fig, ax = qml.draw_mpl(circuit)()
fig.show()
Работая с библиотекой PennyLane для математических операций, можно использовать интерфейс NumPy, но при этом также пользоваться преимуществами автоматического дифференцирования, которое обеспечивает autograd.
Именно поэтому мы не импортировали NumPy обычным способом: import numpy as np, а сделали это так: from pennylane import numpy as np.
Второй способ создания квантовых узлов – с помощью декоратора QNode. Пропускаем импорт библиотек и создание устройства, так как в начале код тот же самый:
@qml.qnode(dev)
def circuit():
qml.Hadamard(wires=0)
qml.CNOT(wires=[0, 1])
return qml.probs(wires=[0, 1])
print(circuit())
[0.503 0. 0. 0.497]
В данном примере мы взяли двухкубитную систему и создали запутанное состояние, а затем с помощью метода probs вычислили вероятности получения состояний \(|00\rangle\), \(|01\rangle\), \(|10\rangle\), \(|11\rangle\).
Операторы#
В квантовой функции можно применять операторы X, Y, Z, S, T (qml.PauliX, qml.PauliY, qml.PauliZ, qml.S, qml.T соответственно), а также операторы, в которых можно задавать угол вращения вокруг одной из осей в радианах: qml.RX, qml.RY, qml.RZ. Здесь и далее будем использовать qml как псевдоним библиотеки PennyLane.
В этой функции мы вращаем кубит под индексом 0 вокруг оси X на 90 градусов из начального состояния \(|0\rangle\) и возвращаем ожидаемое значение qml.PauliZ для этого кубита с помощью qml.expval. Вероятности получения состояний \(|0\rangle\) и \(|1\rangle\) равны, так что мы получаем ожидаемое значение, близкое к нулю, что легко проверить:
@qml.qnode(dev)
def circuit(x):
qml.RX(x, wires=0)
return qml.expval(qml.PauliZ(0))
circuit(np.pi/2)
tensor(-0.06, requires_grad=True)
В следующем примере мы вращаем кубит на тот же угол 90 градусов, но уже вокруг оси Y. Ожидаемое значение в этот раз ищем для qml.PauliX и получаем 1, что соответствует вычислениям:
@qml.qnode(dev)
def circuit(x):
qml.RY(x, wires=0)
return qml.expval(qml.PauliX(0))
circuit(np.pi/2)
tensor(1., requires_grad=True)
В начале этого урока мы создали устройство, которое создает и запускает одну и ту же схему 1000 раз, каждый раз производя измерения. Поменяем этот параметр:
dev.shots = 5
Посмотрим на результат каждого из этих пяти запусков и измерений для qml.PauliZ. Квантовая схема будет простой: применим к кубиту с индексом 1 оператор Адамара:
@qml.qnode(dev)
def circuit():
qml.Hadamard(wires=1)
return qml.sample(qml.PauliZ([1]))
circuit()
tensor([ 1, -1, -1, 1, 1], requires_grad=True)
Мы получаем разные результаты: то 1, что соответствует состоянию \(|0\rangle\), то -1, что соответствует состоянию \(|1\rangle\).
Если вместо qml.PauliZ брать сэмплы для qml.PauliX, то результат все время будет один и тот же: 1, что соответствует состоянию \(|+\rangle\) (вектор базиса Адамара).
@qml.qnode(dev)
def circuit():
qml.Hadamard(wires=1)
return qml.sample(qml.PauliX([1]))
circuit()
tensor([1, 1, 1, 1, 1], requires_grad=True)
QubitUnitary#
В PennyLane можно использовать готовые операторы, либо задавать операторы явно с помощью матриц.
Для этого можно использовать класс qml.QubitUnitary, который принимает два параметра: U – квадратную унитарную матрицу и wires – кубиты, на которые действует оператор U.
В качестве примера создадим оператор, осуществляющий обмен состояний между кубитами (SWAP). Такой оператор уже есть в библиотеке PennyLane (qml.SWAP), но мы создадим его с помощью qml.QubitUnitary. Сначала мы зададим саму матрицу в виде двумерного массива, используя интерфейс NumPy:
U = np.array([[1, 0, 0, 0],
[0, 0, 1, 0],
[0, 1, 0, 0],
[0, 0, 0, 1]])
Создадим заново устройство, при этом зададим число запусков схемы как shots=1: чтобы убедиться, что все работает правильно, нам будет достаточно одного запуска.
dev = qml.device("default.qubit", shots=1, wires=2)
Создадим и запустим схему, в которой перед применением операции SWAP, реализованной с помощью qml.QubitUnitary, один кубит будет находиться в состоянии 1, а другой – в состоянии 0.
@qml.qnode(dev)
def circuit(do_swap):
qml.PauliX(wires=0)
if do_swap:
qml.QubitUnitary(U, wires=[0, 1])
return qml.sample(qml.PauliZ([0])), qml.sample(qml.PauliZ([1]))
Запустим схему сначала без применения операции SWAP:
circuit(do_swap=False)
tensor([[-1],
[ 1]], requires_grad=True)
А затем – с применением:
circuit(do_swap=True)
tensor([[ 1],
[-1]], requires_grad=True)
Видим, что во втором случае операция SWAP сработала: состояния кубитов поменялись местами. Можно посмотреть, как выглядит такая схема:
fig, ax = qml.draw_mpl(circuit)(True)
fig.show();