Квантовый бит#

Автор(ы):

Описание лекции#

Эта лекция расскажет:

  • что такое кубит;

  • в чем разница между значением и состоянием;

  • что такое сфера Блоха;

  • какие можно делать операции над кубитами;

  • что такое измерение.

Введение#

Это первая лекция основного блока нашего курса. Прежде чем мы начнем детально разбирать понятие кубита, давайте взглянем на общий пайплайн квантовых схем.

../../../_images/any_qubit_diagram.svg

Fig. 19 Схема любого квантового алгоритма#

Любая квантовая схема включает в себя:

  • кубиты, инициализируемые в начальное состояние, обычно \(\ket{0}\);

  • унитарные и обратимые операции над кубитами;

  • измерение кубитов.

Эта лекция посвящена разбору операций для одного кубита. Начнем с понятия кубита и его отличий от бита классических компьютеров.

Что такое кубит#

Классический компьютер оперирует двоичными числами – нулем и единицей. Минимальный объем информации для классического компьютера называется бит. Квантовый компьютер оперирует квантовыми битами или кубитами, которые тоже имеют два возможных значения – 0 и 1. Так в чем же разница? В чем особенности квантовых компьютеров, которые дают им преимущества над классическими компьютерами?

Разница в том, что для квантовомеханических систем (и кубитов в частности) их состояния и значения – это не одно и то же.

Состояние vs значение#

Состояние классического бита#

Обычно мы не отличаем состояние классического бита от его значения и считаем, что если бит имеет значение 1, то и состояние его описывается числом 1.

Кот Шредингера#

Давайте вспомним мысленный эксперимента Шредингера. Кот, который одновременно и жив, и мертв. Понятно, что значение кота точно одно: он либо жив, либо мертв. Но состояние его более сложное. Он находится в суперпозиции состояний “жив” и “мертв” одновременно.

../../../_images/Schrodingers_cat.png

Fig. 20 Кот Шредингера#

Состояние кубита#

Состояние кубита, если можно так сказать, аналогично состоянию кота Шредингера. Оно отличается от значения кубита и описывается вектором из двух комплексных чисел. Мы будем обозначать состояния (или вектора) символом \(\ket{\Psi}\) (кет – вектор-столбец) – это широко принятая в квантовой механике и квантовых вычислениях нотация Дирака:

\[\begin{split} \ket{\Psi} = \begin{bmatrix} c_0 \\ c_1 \end{bmatrix} \end{split}\]

Note

Может возникнуть вопрос, а почему комплексные числа? Короткий ответ на этот вопрос дать сложно. Если в двух словах, то использование комплексных чисел связано с удобством представления матричных групп, используемых в квантовой механике.

Все еще звучит сложно? Тогда нужно вспомнить, что изначально квантовая механика возникла в том числе из-за того, что физики экпериментально обнаружили у фундаментальных частиц свойство корпускулярно-волнового дуализма. Иными словами, электроны, фотоны и другие частицы проявляли как типичные свойства волнового движения (например, интерференцию и дифракцию), и свойства частиц – например, всегда есть минимальная порция (квант!) света или электрического поля. Кстати, часто вместо вектора состояния используется понятие волновой функции, которая описывает плотность вероятности обнаружить частицу в той или иной точке пространства (обычного или специального). Ко времени создания квантовой механики для описания волнового движения ученые уже привыкли использовать комплескные числа, которые позволяют упростить описание многих эффектов за счет разделения амплитуды и фазы процесса. Такое удобство справедливо и для многих задач квантовой физики.

Для более детального ответа авторы курса рекомендуют читать книги по истории квантовой физики (и по самой квантовой физике).

Значение чисел \(c_0\) и \(c_1\) мы обсудим чуть позже, а пока запишем наш кубит \(\ket{\Psi}\) в коде Python. Для начала \(c_0 = c_1 = \frac{1}{\sqrt{2}}\).

import numpy as np
qubit = np.array([1 / np.sqrt(2) + 0j, 1 / np.sqrt(2) + 0j]).reshape((2, 1))

Здесь мы создаем именно вектор-столбец размерности \(2 \times 1\).

\[\begin{split} \ket{\Psi} = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} \end{split}\]
print(qubit.shape)

(2, 1)

Связь состояния и значения кубита#

Разберем подробнее вектор \(\ket{\Psi}\) и значение цифр \(c_0, c_1\). Посмотрим на состояния кубита, значение которого мы знаем точно. То есть “посмотрим на кота Шредингера”, но который точно жив или точно мертв.

Базисные состояния#

Посмотрим, как выглядят состояния кубитов с точно определенными значениями:

\[\begin{split} \ket{0} = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \text{\qquad} \ket{1} = \begin{bmatrix} 0 \\ 1 \end{bmatrix} \end{split}\]

Что мы можем сказать об этих состояниях? Как минимум следующее:

  • они ортогональны (\(\ket{0} \perp \ket{1}\));

  • они имеют единичную норму;

  • они образуют базис.

Что это значит для нас? А то, что любое состояние \(\ket{\Psi}\) можно записать как линейную комбинацию векторов \(\ket{0}\) и \(\ket{1}\), причем коэффициентами в этой комбинации будут как раз \(c_0, c_1\):

basis_0 = np.array([1 + 0j, 0 + 0j]).reshape((2, 1))
basis_1 = np.array([0 + 0j, 1 + 0j]).reshape((2, 1))

c0 = c1 = 1 / np.sqrt(2)

print(np.allclose(qubit, c0 * basis_0 + c1 * basis_1))

True
\[\begin{split} \ket{\Psi} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 0 \end{bmatrix} + \frac{1}{\sqrt{2}} \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} \end{split}\]

Амплитуды вероятностей#

Квантовая механика устроена таким интересным образом, что если мы будем измерять значение кубита, то вероятность каждого из вариантов будет пропорциональна соответствующему коэффициенту в разложении состояния. Но так как амплитуды – это в общем случае комплексные числа, а вероятности должны быть строго действительные, нужно домножить амплитуды на комплексно сопряженные значения. В случае наших значений \(c_0 = c_1 = \frac{1}{\sqrt{2}}\) получаем:

p0 = np.conj(c0) * c0
p1 = np.conj(c1) * c1

print(np.allclose(p0, p1))
print(np.allclose(p0 + p1, 1.0))

True
True

Видим еще одну важную вещь: сумма вероятностей всех состояний должна быть равна 100%. Это сразу приводит нас к тому, что состояния – это не любые комплексные вектора, а комплексные вектора с единичной нормой:

print(np.allclose(np.conj(qubit).T @ qubit, 1.0))

True
\[\begin{split} \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} = 1.0 \end{split}\]

Мы будем очень часто пользоваться транспонированием и взятием комплексно сопряженного от векторов. В квантовой механике это имеет специальное обозначение \(\bra{\Psi} = {\Psi^T}^* = \Psi^\dagger\) (бра – вектор-строка). Тогда наше правило нормировки из NumPy кода может быть записано в нотации Дирака так:

\[ \braket{\Psi | \Psi} = 1 \]

Сфера Блоха#

Описанный выше базис \(\ket{0}, \ket{1}\) не является единственно возможным. Вектора \(\ket{0}, \ket{1}\) – это лишь самый часто применимый базис, который называют \(\mathbf{Z}\) базисом. Но есть и другие варианты.

Возможные базисы#

Z-базис#

Уже описанные нами \(\ket{0}\) и \(\ket{1}\).

X-базис#

Базисные состояния \(\ket{+} = \frac{\ket{0} + \ket{1}}{\sqrt{2}}\) и \(\ket{-} = \frac{\ket{0} - \ket{1}}{\sqrt{2}}\):

plus = (basis_0 + basis_1) / np.sqrt(2)
minus = (basis_0 - basis_1) / np.sqrt(2)

Y-базис#

Базисные состояния \(\ket{R} = \frac{\ket{0} + i\ket{1}}{\sqrt{2}}\) и \(\ket{L} = \frac{\ket{0} - i\ket{1}}{\sqrt{2}}\):

R = (basis_0 + 1j * basis_1) / np.sqrt(2)
L = (basis_0 - 1j * basis_1) / np.sqrt(2)

Легко убедиться, что все вектора каждого из этих базисов ортогональны:

print(np.allclose(np.conj(basis_0).T @ basis_1, 0))

True
\[\begin{split} \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} 0 \\ 1 \end{bmatrix} = 0 \end{split}\]
print(np.allclose(np.conj(plus).T @ minus, 0))

True
\[\begin{split} \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \end{bmatrix} = 0 \end{split}\]
print(np.allclose(np.conj(R).T @ L, 0))

True
\[\begin{split} \begin{bmatrix} \frac{1}{\sqrt{2}} & -i\frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} \\ -i\frac{1}{\sqrt{2}} \end{bmatrix} = 0 \end{split}\]

Заметьте, что в наших векторных пространствах скалярное произведение – это (в случае действительных векторов) \(\vec{a}\vec{b} = \left\langle a\middle| b\right\rangle\) (бра-кет). Именно поэтому нужно делать транспонирование и комплексное сопряжение первого вектора в паре.

Сфера Блоха#

Обозначения \(\ket{0}, \ket{1}, \ket{+}, \ket{-}, \ket{R}, \ket{L}\) выбраны неслучайно: они имеют геометрический смысл.

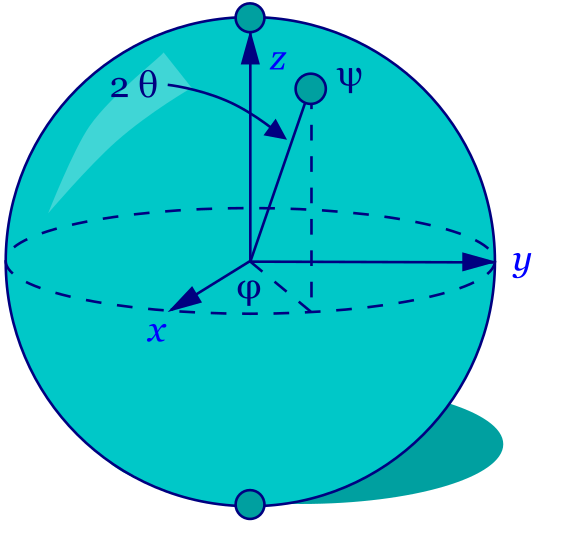
../../../_images/Blochsphere.png

Fig. 21 Сфера Блоха#

Принято считать, что ось \(\mathbf{Z}\) – это основная ось, так как физически квантовые компьютеры измеряют именно по ней. Ось \(\mathbf{X}\) “смотрит на нас” и поэтому обозначается \(\ket{+}\) и \(\ket{-}\). А ось \(\mathbf{Y}\) направлена как бы вдоль, поэтому базис обозначают как “право” (\(\ket{R}\)) и “лево” (\(\ket{L}\)).

Вектор состояния кубита еще называют волновой функцией, и этот вектор может идти в любую точку сферы Блоха. Сама сфера имеет единичный радиус, и это гарантирует нам, что для всех состояний сумма квадратов амплитуд будет равна единице.

Состояние в полярных координатах#

Состояние кубита можно выразить через полярные координаты на сфере Блоха:

\[ \ket{\Psi} = c_0 \ket{0} + c_1 \ket{1} = \cos\theta\ket{0} + e^{i\phi}\sin\theta \ket{1}, \]

где \(\theta,\phi\) – это угловые координаты на сфере Блоха. В этом смысле сфера Блоха очень удобна для представления состояний одного кубита.

Note

Тут мы воспользовались формулой Эйлера, а также вынесли за скобки локальные фазы множителей \(c_0\) и \(c_1\). Если у вас возникают трудности с подобными операциями над комплексными числами, то рекомендуем еще раз пересмотреть базовый блок нашего курса по линейной алгебре и комплексным числам, там эти моменты освещаются более подробно.

Что можно делать с таким кубитом?#

Линейные операторы#

Любое действие, которое мы совершаем с кубитом в состоянии \(\ket{\Psi}\), должно переводить его в другое состояние \(\ket{\Phi}\). Что переводит один вектор в другой вектор в том же пространстве? Правильно, матрица. Другими словами, линейный оператор. Мы будем обозначать операторы как \(\hat{U}\).

Унитарность#

Как мы уже говорили, квадраты амплитуд – это вероятности. Следовательно, волновая функция должна быть нормирована на единицу. А значит, любой оператор, который переводит одно состояние в другое \(\hat{U}\ket{\Psi} = \ket{\Phi}\), должен сохранять эту нормировку, то есть должен быть унитарным. Более того, свойство унитарности приводит к тому, что любой квантовый оператор еще и сохраняет скалярное произведение:

\[ \bra{\Psi}\hat{U}^\dagger\hat{U}\ket{\Psi} = \bra{\Psi}\ket{\Psi} \]

Другими словами, унитарный оператор удовлетворяет условию \(\hat{U}^\dagger \hat{U} = \hat{I}\).

Обратимость#

Одно из важных следствий унитарности операций над кубитами – это их обратимость. Если вы сделали какую-то последовательность унитарных операций над кубитами \(\hat{U}\), то их можно вернуть в начальное состояние, ведь у унитарного оператора всегда есть обратный оператор \(\hat{U}^{-1} = \hat{U}^\dagger\).

Note

Квантовый компьютер должен уметь делать несколько не унитарных операций, например, инициализацию кубита в определенное состояние (например, \(\ket{0}\)) и считывание состояния кубитов. Такие неунитарные операции приводят к потере информации и являются необратимыми.

Пример оператора#

В дальнейших лекциях мы разберем много операторов, так как именно операторы (или квантовые гейты) являются основой квантовых вычислений. А пока рассмотрим простой пример: оператор Адамара (Hadamard gate), который переводит \(\ket{0} \to \ket{+}\).

Гейт Адамара#

Начнем с того, что пока у нас лишь один кубит. Состояние одного кубита – это вектор размерности два. Значит, оператор, который переводит его в другой вектор размерности два – это матрица \(2\times 2\). Запишем оператор Адамара в матричном виде, а потом убедимся, что он унитарный и действительно переводит состояние \(\ket{0} \to \ket{+}\).

\[\begin{split} \hat{H} = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \\ \end{bmatrix} \end{split}\]
Реализация в Python#
h = 1 / np.sqrt(2) * np.array([
    [1 + 0j, 1 + 0j],
    [1 + 0j, 0j - 1]
])
Унитарность#
print(np.allclose(np.conj(h).T @ h, np.eye(2)))

True
\[\begin{split} \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \\ \end{bmatrix} \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} \end{split}\]
Проверка#

Проверим, что гейт Адамара действительно переводит кубит из состояния \(\ket{0}\) в состояние \(\ket{+}\).

print(np.allclose(h @ basis_0, plus))

True
\[\begin{split} \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \\ \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} \end{split}\]

Измерение#

Измерение в квантовых вычислениях выделяется отдельно именно потому, что оно “открывает” коробку с котом Шредингера: мы точно узнаем, жив он или мертв, и уже никогда не сможем это “забыть” обратно. Вся суперпозиция его состояния исчезает. То есть измерение – это как раз пример одной из не унитарных операций, которые должен уметь делать квантовый компьютер.

Note

Это интересный факт: исчезновение суперпозиции многим кажется парадоксом, именно поэтому и появляются разные интерпретации квантовой механики, например, многомировая интерпретация Эверетта. Действительно, это кажется немного странным, что полностью обратимая квантовая механика и непрерывная динамика волновых функций вдруг “ломаются” и мы получаем такой коллапс, который еще называют редукцией фон Неймана. Доктору Эверетт тоже это не нравилось и он предложил другую интерпретацию этого процесса. Согласно его теории, когда мы производим измерения, мы как бы “расщепляем” нашу вселенную на две ниточки: в одной кот остается жив, а в другой остается мертв.

Такие теории остаются на уровне спекуляций, так как почти невозможно придумать эксперимент, который бы подтверждал или опровергал такую гипотезу. Скорее это вопрос личного понимания и интерпретации процесса, так как математически подобные теории в итоге дают один и тот же наблюдаемый и измеримый результат.

Как мы уже говорили, состояние кубита может быть записано в разных базисах: \(\ket{0}, \ket{1}\), \(\ket{+}, \ket{-}\), \(\ket{R}, \ket{L}\). Значение кубита в каждом из этих базисов может быть измерено. Но что такое измерение с точки зрения математики?

Операторы Паули#

На самом деле, любая наблюдаемая величина соответствует какому-то оператору. Например, измерения в разных базисах \(\mathbf{X}\), \(\mathbf{Y}\), \(\mathbf{Z}\) соответствуют операторам Паули:

\[\begin{split} \hat{\sigma}^x = \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix} \qquad \hat{\sigma}^y = \begin{bmatrix} 0 & -i\\ i & 0 \end{bmatrix} \qquad \hat{\sigma}^z = \begin{bmatrix} 1 & 0\\ 0 & -1 \end{bmatrix} \end{split}\]
pauli_x = np.array([[0 + 0j, 1 + 0j], [1 + 0j, 0 + 0j]])
pauli_y = np.array([[0 + 0j, 0 - 1j], [0 + 1j, 0 + 0j]])
pauli_z = np.array([[1 + 0j, 0 + 0j], [0 + 0j, 0j - 1]])

Эти операторы очень важны, рекомендуется знать их наизусть, так как они встречаются в каждой второй статье по квантовым вычислениям, а также постоянно фигурируют в документации всех основных библиотек для квантового машинного обучения.

Собственные значения#

Мы поняли, что есть связь между нашими измерениями и операторами. Но какая именно? Что значит, например, что измерения по оси \(\mathbf{Z}\) соответствуют оператору \(\hat{\sigma}^z\)?

Здесь мы приходим к собственным значениям операторов. Оказывается (так устроен наш мир), что измеряя какую-то величину в квантовой механике, мы всегда будем получать одно из собственных значений соответствующего оператора, а состояние будет коллапсировать в соответствующий собственный вектор этого оператора. Другими словами, измеряя кота Шредингера, мы будем получать значения “жив” или “мертв”, а состояние кота будет переходить в состояние, соответствующее одному из этих значений. А еще измерение не является обратимой операцией: однажды открыв коробку с котом и поняв, жив он или мертв, мы уже не сможем закрыть ее обратно и вернуть кота в суперпозицию.

Описанное выше – не абстрактные рассуждения из квантовой физики. Оно пригодится, когда мы будем говорить о решении практических комбинаторных задач, таких как задача о выделении сообществ в графе.

Собственные вектора \(\hat{\sigma}^z\)#

Вернемся к нашему оператору \(\hat{\sigma}^z\). Легко убедиться, что его собственные значения равны 1 и -1, а соответствующие им собственные вектора – это \(\begin{bmatrix}1 \\ 0\end{bmatrix}\) и \(\begin{bmatrix}0 \\ 1\end{bmatrix}\):

print(np.linalg.eig(pauli_z))

(array([ 1.+0.j, -1.+0.j]), array([[1.+0.j, 0.+0.j],
       [0.+0.j, 1.+0.j]]))

Таким образом, измерение по оси \(\mathbf{Z}\) всегда будет давать нам одно из этих двух значений и переводить состояние кубита в соответствующий собственный вектор.

Caution

Зачастую кубиты измеряют именно в в \(\mathbf{Z}\)-базисе; является неким “стандартом” для квантовых вычислений, так как это измерение “ближе к железу”. Также \(\mathbf{Z}\)-базис удобен для нас из-за диагональности оператора Паули \(\sigma^z\).

Формальная запись#

Формально мы можем записать для любого эрмитова оператора \(\hat{U}\), что собственные состояния этого оператора являются его собственными векторами, а собственные значения в этом случае являются наблюдаемыми значениями:

\[ \hat{U}\ket{\Psi} = u\ket{\Psi} \]

Другие операторы Паули#

Убедимся, что у остальных операторов собственные значения такие же:

print(np.linalg.eig(pauli_x))
print(np.linalg.eig(pauli_y))

(array([ 1.+0.j, -1.+0.j]), array([[ 0.70710678-0.j,  0.70710678+0.j],
       [ 0.70710678+0.j, -0.70710678-0.j]]))
(array([ 1.+0.j, -1.+0.j]), array([[-0.        -0.70710678j,  0.70710678+0.j        ],
       [ 0.70710678+0.j        ,  0.        -0.70710678j]]))

Note

Заметим, что собственные вектора могут отличаться на какой-то множитель. В частности, один из собственных векторов оператора \(\hat{\sigma}^y\), возвращенный np.linalg.eig равен \(\frac{1}{\sqrt{2}} \begin{bmatrix} -i \\ 1 \end{bmatrix}\), что отличается от \(\ket{R} = \frac{\ket{0} + i\ket{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ i \end{bmatrix}\) только домножением на \(i\).

Во-первых, по курсу линейной алгебры мы знаем, что собственные вектора можно домножать на любую константу и они все равно останутся собственными, поскольку если вектор \(x^*\)– решение уравнения \(Ax^* = \lambda x^*\), то и любой вектор \(kx^*, k \in \mathbb{С}, k \neq 0\) также будет решением этого уравнения.

Во-вторых, состояния, отличающиеся только множителем, по сути соответствуют одному и тому же состоянию. Любой множитель \(c \in \mathbb{С}\), стоящий перед вектором состояния \(\ket{\Psi}\) можно представить в виде \(c = e^{i\phi}\), что соответствует повороту на некоторый угол \(\phi\). При вычислении амплитуды \({|\ket{\Psi}|} ^ 2\) этот множитель даст единицу, то есть, другими словами, поворот кубита никак не повлияет на результат измерения кубита. Это известно как глобальная фаза, и в научной литературе часто можно встретить фразу “up to a global phase factor”, что означает одинаковые состояния с точностью до поворота (примерно как произвольная константа, добавляемая к интегралу).

Note

Также можно заметить, что у всех операторов Паули нет ни одного общего собственного вектора. Таким образом, мы приходим к ситуации, когда не можем одновременно точно провести измерения двумя разными операторами, так как наше измерение должно переводить состояние в соответствующий собственный вектор. В квантовой механике это называется принципом неопределенности.

Ожидаемое значение при измерении#

Мы не будем писать с нуля полный симулятор кубитов, который включает измерения – это требует введения сложного случайного процесса. Но мы можем легко ответить на другой вопрос. А именно: можно ли сказать, какое будет ожидаемое значение оператора \(\hat{U}\) для состояния \(\Psi\)? Другими словами, какое будет математическое ожидание большого числа измерений? Это можно записать следующим образом:

\[ \mathbf{E}(\hat{U}) = \bra{\Psi}\hat{U}\ket{\Psi} \]

Например, оператор \(\hat{\sigma}^z\) полностью не определен в состоянии \(\ket{+}\), то есть мы будем равновероятно получать значения -1 и 1, а математическое ожидание, соответственно, будет равно нулю:

print(plus.conj().T @ pauli_z @ plus)

[[-2.23711432e-17+0.j]]
\[\begin{split} \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} = 0 \end{split}\]

С другой стороны, измеряя состояние \(\ket{+}\) в X-базисе мы всегда будем получать 1:

print(plus.conj().T @ pauli_x @ plus)

[[1.+0.j]]
\[\begin{split} \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} = 1 \end{split}\]

Вероятности битовых строк#

Последнее, чего мы коснемся в части измерений – это битовые строки и метод Шредингера. Мы много говорили о вероятностной интерпретации волновой функции и аналогиях с классическим битом, но пока этого никак не касались на практике. Как же получить вероятность определенной битовой строки для произвольного состояния? Если взять все битовые строки размерности вектора состояния и отсортировать их в лексикографическом порядке (например, \(0 < 1\), \(00 < 01 < 10 < 11\), и т.д.), то вероятность каждой битовой строки получается следующим выражением:

\[ \mathbf{P} = | \bra{\Psi}\ket{\vec{s}} |^2, \]

где \(\vec{s}\) – это вектор, каждая компонента которого соответствует порядковой битовой строке или вектор битовых строк. Другими словами, вероятность получить i-ю битовую строку равна квадрату i-го элемента амплитуды волновой функции. Кажется немного запутанным, но на самом деле \(|\ket{\Psi}|^2\) – это идейно и есть плотность вероятности.

Еще пара слов об измерениях#

Измерение как проекция на пространство собственных векторов#

Мы уже говорили, что при измерении мы как бы “выбираем” один из собственных векторов наблюдаемой. Более строго такой процесс называется проецированием на пространство собственных векторов. Для собственного вектора \(\ket{\Phi}\) проекция будет линейным оператором:

\[ \hat{P}_{\ket{\Phi}} = \ket{\Phi}\bra{\Phi} \]
super_position = h @ basis_0
eigenvectors = np.linalg.eig(pauli_z)[1]

proj_0 = eigenvectors[0].reshape((-1, 1)).conj() @ eigenvectors[0].reshape((1, -1))
proj_1 = eigenvectors[1].reshape((-1, 1)).conj() @ eigenvectors[1].reshape((1, -1))

Убедимся что это действительно проекция:

print(np.allclose(proj_0 @ proj_0, proj_0), np.allclose(proj_1 @ proj_1,proj_1))

True True
\[\begin{split} \hat{P}_{\ket{\Phi_0}} = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \otimes \begin{bmatrix} 1 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 0 \\ \end{bmatrix} \end{split}\]
\[\begin{split} \hat{P}_{\ket{\Phi_1}} = \begin{bmatrix} 0 \\ 1 \end{bmatrix} \otimes \begin{bmatrix} 0 & 1 \end{bmatrix} = \begin{bmatrix} 0 & 0 \\ 0 & 1 \\ \end{bmatrix} \end{split}\]

Note

Измерения в квантовой механике не обязательно проективные. В более общем случае рассматриваем набор операторов \(\{ E_i \}\) выполняющий следующие условия:

  1. Эрмитовость (\(E^\dagger_i = E_i\))

  2. Неотрицательность (\(\bra{\psi} E_i \ket{ \psi } \geq 0\) для любого \(\ket{\Psi}\))

  3. Полнота (\(\sum_i E_i = I\)).

Такой набор называется positive operator-valued measure (POVM). Так как оператор \(E_i\) неотрицательный и эрмитов, мы можем найти его “квадратный корень”: \(M_i^\dagger M_i = E_i\), и вероятность определенного результата равна \(\bra{\psi} E_i \ket{ \psi } \). В случае проективных измерений \(M_i = \hat{P}_{\ket{\Phi}}\).

Правило Борна#

Как мы уже говорили, любому эрмитову оператору соответствует какая-либо наблюдаемая величина. А какая наблюдаемая величина соответствует оператору проекции на собственный вектор \(\ket{\Phi}\), про который мы говорили выше? Ответ – вероятность наблюдения собственного значения, которое соответствует этому собственному вектору. Значит, чтобы получить вероятность измерения значения \(\lambda_i\) эрмитова оператора \(\hat{A}\) (которое соответствует собственному вектору \(\ket{\Phi_i}\) этого оператора) в состоянии \(\ket{\Psi}\), мы должны измерить величину \(\bra{\Psi} \hat{P}_{\ket{\Phi_i}} \ket{\Psi}\). Это называется правилом Борна.

\[ \mathbf{P}(\lambda_i) = \bra{\Psi} \hat{P}_{\ket{\Phi_i}} \ket{\Psi} \]

Считать ожидаемое значение оператора мы уже умеем. Давайте убедимся, что для состояния \(\ket{\Psi} = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ 1\end{bmatrix}\) результаты измерений операторов проекций дадут 0.5 и совпадут с результатом упражнения, которое мы проделали ранее:

p_0 = super_position.conj().T @ proj_0 @ super_position

print(np.allclose(p_0, 0.5))

True
\[\begin{split} \mathbf{P}(\lambda_0) = \Bigg( \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 0 \\ \end{bmatrix} \Bigg) \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} \Bigg( \begin{bmatrix} 1 & 0 \\ 0 & 0 \\ \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} \Bigg) = \frac{1}{2} \end{split}\]
p_1 = super_position.conj().T @ proj_1 @ super_position

print(np.allclose(p_1, 0.5))
print(np.allclose(p_0 + p_1, 1.0))

True
True
\[\begin{split} \mathbf{P}(\lambda_1) = \Bigg( \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} 0 & 0 \\ 0 & 1 \\ \end{bmatrix} \Bigg) \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} \Bigg( \begin{bmatrix} 0 & 0 \\ 0 & 1 \\ \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} \Bigg) = \frac{1}{2} \end{split}\]

Что мы узнали?#

  • Состояние и значение для кубита – это не одно и то же.

  • Состояния представляют собой комплекснозначные вектора.

  • Квантовые операторы – унитарные и самосопряженные.

  • Измеряемые значения – собственные значения операторов.

  • Измерение “ломает” суперпозицию.