Квантовые гейты#

Автор(ы):

Описание лекции#

Из этой лекции мы узнаем:

  • какие есть основные однокубитные и многокубитные гейты;

  • как записывать многокубитные состояния;

  • как конструировать многокубитные операторы;

  • как работать с библиотекой PennyLane.

Введение#

Квантовые гейты являются основными строительными блоками для любых квантовых схем, в том числе и тех, что применяются для машинного обучения. Можно сказать, что это своеобразный алфавит квантовых вычислений. Он необходим, чтобы сходу понимать, например, что изображено на подобных схемах:

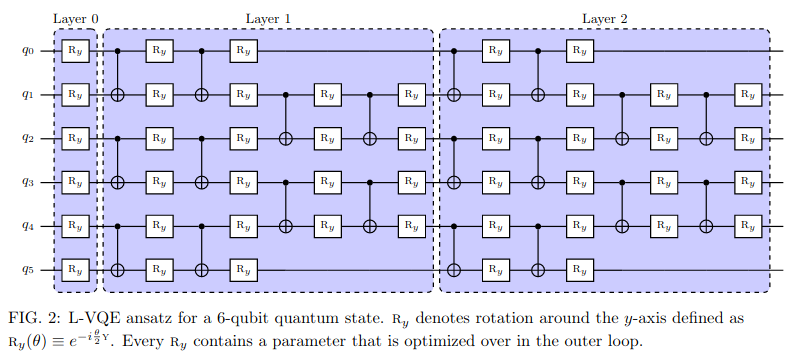
../../../_images/Layer-VQE.png

Fig. 22 Схема Layered-VQE#

Основные однокубитные гейты#

В прошлый раз мы познакомились с операторами Паули, а также гейтом Адамара. Как для обычных квантовых алгоритмов, так и для QML-алгоритмов нужны и другие гейты, потому что одни только эти гейты не позволяют перейти во все возможные квантовые состояния. Теперь давайте посмотрим, какие еще однокубитные гейты часто применяются в квантовых вычислениях и квантовом машинном обучении.

T-гейт#

T-гейт очень популярен в универсальных квантовых вычислениях. Его матрица имеет вид:

\[\begin{split} \hat{T} = \begin{bmatrix} 1 & 0 \\ 0 & \frac{1+i}{\sqrt{2}} \end{bmatrix} \end{split}\]

Любой однокубитный гейт можно аппроксимировать последовательностью гейтов Адамара и T-гейтов. Чем точнее требуется аппроксимация, тем длиннее будет аппроксимирующая последовательность.

Помимо важной роли в математике квантовых вычислений, гейт Адамара и T-гейт интересны тем, что именно на них построено большинство предложений по реализации квантовых вычислений с топологической защитой или с коррекцией ошибок. На сегодняшний день эти схемы реально пока не очень работают: никаких топологически защищенных кубитов продемонстрировано не было, а коррекция ошибок не выходит за пределы двух логических кубитов.

Гейты поворота вокруг оси#

Поворотные гейты играют центральную роль в квантовом машинном обучении. Вспомним на секунду, как выглядят наши однокубитные состояния на сфере Блоха:

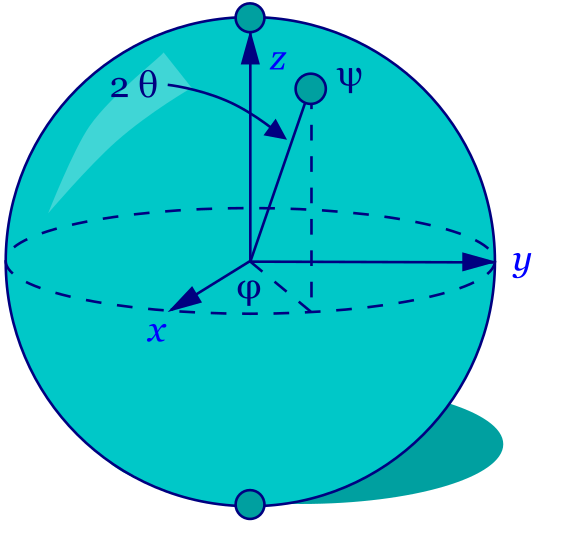
../../../_images/Blochsphere.png

Fig. 23 Сфера Блоха#

Любой однокубитный гейт можно представить как вращение вектора состояния \(\ket{\Psi}\) на некоторый угол вокруг некоторой оси, проходящей через центр сферы Блоха.

Гейты \(\hat{RX}(\phi), \hat{RY}(\phi), \hat{RZ}(\phi)\) осуществляют поворот на определенный угол \(\phi\) вокруг соответствующей оси на сфере Блоха.

Давайте внимательно рассмотрим это на примере гейта \(\hat{RY}\).

Гейт \(\hat{RY}\)#

Сам гейт определяется следующим образом:

\[\begin{split} \hat{RY}(\phi) = \begin{bmatrix} \cos(\frac{\phi}{2}) & -\sin(\frac{\phi}{2}) \\ \sin(\frac{\phi}{2}) & \cos(\frac{\phi}{2}) \end{bmatrix} \end{split}\]
import numpy as np

def ry(state, phi):
    return np.array([
        [np.cos(phi / 2), -np.sin(phi / 2)],
        [np.sin(phi / 2),  np.cos(phi / 2)]
    ]) @ state

Запишем наше состояние \(\ket{0}\):

basis = np.array([1 + 0j, 0 + 0j]).reshape((2, 1))

Внимательно посмотрим на сферу Блоха. Можно заметить, что если повернуть состояние из \(\ket{0}\) на \(\frac{\pi}{2}\) и измерить значение \(\hat{\sigma^x}\), то получится 1. А если повернуть на \(-\frac{\pi}{2}\), то получится -1:

def expval(state, op):
    return state.conj().T @ op @ state

pauli_x = np.array([[0 + 0j, 1 + 0j], [1 + 0j, 0 + 0j]])

print(np.allclose(expval(ry(basis, np.pi / 2), pauli_x), 1.0))
print(np.allclose(expval(ry(basis, -np.pi / 2), pauli_x), -1.0))

True
True

Убедимся также, что вращение на угол, пропорциональный \(2\pi\), не меняет результат измерения. Возьмем случайное состояние:

\[\begin{split} \ket{\Psi} = \begin{bmatrix} 0.42 \\ \sqrt{1 - 0.42^2} \end{bmatrix} \end{split}\]
random_state = np.array([0.42 + 0j, np.sqrt(1 - 0.42**2) + 0j]).reshape((2, 1))

Измерим его по осям \(\mathbf{X}\) и \(\mathbf{Z}\), затем повернем на угол \(2\pi\) и измерим снова:

pauli_z = np.array([[1 + 0j, 0 + 0j], [0 + 0j, 0j - 1]])

print("Z:\n\t" + str(expval(random_state, pauli_z)) + "\n")
print("X:\n\t" + str(expval(random_state, pauli_x)) + "\n")

print("Z after RY:\n\t" + str(expval(ry(random_state, 2 * np.pi), pauli_z)) + "\n")
print("X after RY:\n\t" + str(expval(ry(random_state, 2 * np.pi), pauli_x)) + "\n")

Z:
	[[-0.6472+0.j]]

X:
	[[0.76232025+0.j]]

Z after RY:
	[[-0.6472+0.j]]

X after RY:
	[[0.76232025+0.j]]

Другие гейты вращений#

Аналогичным образом определяются гейты \(\hat{RX}\) и \(\hat{RZ}\):

\[\begin{split} \hat{RX}(\phi) = \begin{bmatrix} \cos(\frac{\phi}{2}) & -i\sin(\frac{\phi}{2}) \\ -i\sin(\frac{\phi}{2}) & \cos(\frac{\phi}{2}) \end{bmatrix} \qquad \hat{RZ}(\phi) = \begin{bmatrix} e^{-\frac{i\phi}{2}} & 0 \\ 0 & e^{\frac{i\phi}{2}} \end{bmatrix} \end{split}\]

Общая форма записи однокубитных гейтов#

В общем случае однокубитные гейты могут быть также записаны следующим образом:

\[ \large \hat{R}^\vec{n}(\alpha) = e^{-\frac{i\alpha\hat{\vec{\sigma}}\vec{n}}{2}}, \]

где \(\alpha\) – это угол поворота, \(\vec{n}\) – единичный вектор в направлении оси поворота, а \(\hat{\vec{\sigma}} = \{\hat{\sigma}^x, \hat{\sigma}^y, \hat{\sigma}^z\}\) – это вектор, составленный из операторов Паули. Если использовать покоординатную запись и \(\vec{n} = \{n_x, n_y, n_z\}\) задает ось вращения, то

\[ \large \hat{R}^\vec{n}(\alpha) = e^{-i\frac{\alpha}{2}\left(\hat{\sigma}^xn_x+\hat{\sigma}^yn_y+\hat{\sigma}^zn_z\right)}. \]

Забегая вперед, можно сказать, что именно гейты вращений – это основа квантовых вариационных схем, главного инструмента этого курса.

Phase-shift гейт#

Другой важный гейт – это так называемый phase-shift гейт, или \(\hat{U}_1\) гейт. Его матричная форма имеет следующий вид:

\[\begin{split} \hat{U}_1(\phi) = \begin{bmatrix} 1 & 0 \\ 0 & e^{i\phi} \end{bmatrix} \end{split}\]
def u1(state, phi):
    return np.array([[1, 0], [0, np.exp(1j * phi)]]) @ state

Легко видеть, что с точностью до глобального фазового множителя, который ни на что не влияет, Phase-shift-гейт – это тот же \(\hat{RZ}(\phi)\). Он играет важную роль в квантовых ядерных методах.

Гейты \(\hat{U}_2\) и \(\hat{U}_3\)#

Более редкие в QML гейты, которые однако все равно встречаются в статьях.

\[\begin{split} \hat{U}_2(\phi, \lambda) = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & -e^{i\lambda} \\ e^{i\phi} & e^{i(\phi + \lambda)} \end{bmatrix} = \hat{U}_1(\phi + \lambda)\hat{RZ}(-\lambda)\hat{RY}(\frac{\pi}{2})\hat{RZ}(\lambda) \end{split}\]

Давайте убедимся в справедливости этого выражения:

def rz(state, phi):
    return np.array([[np.exp(-1j * phi / 2), 0], [0, np.exp(1j * phi / 2)]]) @ state


def u2_direct(phi, l):
    return (
        1
        / np.sqrt(2)
        * np.array([[1, -np.exp(1j * l)], [np.exp(1j * phi), np.exp(1j * (phi + l))]])
    )


def u2_inferenced(phi, l):
    return (
        u1(np.eye(2), phi + l)
        @ rz(np.eye(2), -l)
        @ ry(np.eye(2), np.pi / 2)
        @ rz(np.eye(2), l)
    )

print(np.allclose(u2_direct(np.pi / 6, np.pi / 3), u2_inferenced(np.pi / 6, np.pi / 3)))

True

Схожим образом определяется \(\hat{U}_3(\theta, \phi, \lambda)\):

\[\begin{split} \hat{U}_3(\theta, \phi, \lambda) = \begin{bmatrix} \cos(\frac{\theta}{2}) & -e^{1j\lambda}\sin(\frac{\theta}{2}) \\ e^{1j\phi}\sin(\frac{\theta}{2}) & e^{1j(\phi + \lambda)}\cos(\frac{\theta}{2}) \end{bmatrix} = \hat{U}_1(\phi + \lambda)\hat{RZ}(-\lambda)\hat{RY}(\theta)\hat{RZ}(\lambda) \end{split}\]

Читатель может сам легко убедиться, что эти формы записи эквивалентны. Для этого надо написать примерно такой же код, что мы писали раньше для \(\hat{U}_2\).

Еще пара слов об однокубитных гейтах#

На этом мы завершаем обзор основных однокубитных гейтов. Маленькое замечание: гейты, связанные со сдвигом фазы, никак не меняют состояние кубита, если оно сейчас \(\ket{0}\). Так как мы всегда предполагаем, что начальное состояние кубитов – это именно \(\ket{0}\), то перед применением, например, \(\hat{U}_1\), рекомендуется применить гейт Адамара:

print(np.allclose(u1(basis, np.pi / 6), basis))

h = 1 / np.sqrt(2) * np.array([[1 + 0j, 1 + 0j], [1 + 0j, 0j - 1]])
print(np.allclose(u1(h @ basis, np.pi / 6), h @ basis))

True
False

Единичный гейт#

Самое последнее об однокубитных гейтах – это единичный гейт \(\hat{I}\):

\[\begin{split} \hat{I} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \end{split}\]
identity_gate = np.eye(2, dtype=np.complex128)
print(identity_gate)

[[1.+0.j 0.+0.j]
 [0.+0.j 1.+0.j]]

Он не делает с кубитом ровным счетом ничего. Но единичный гейт понадобится нам позже, когда мы будем конструировать многокубитные операторы.

Многокубитные состояния и гейты#

Очевидно, что с одним кубитом ничего интересного, кроме разве что генератора истинно-случайных чисел, мы не сделаем. Для начала разберемся, как выглядят состояния для многокубитных систем.

Многокубитные состояния#

В классическом компьютере один бит имеет два значения – 0 и 1. Два бита имеют четыре значения – 00, 01, 10, 11. Три бита имеют восемь значений и так далее. Аналогично состояние двух кубитов – это вектор в пространстве \(\mathbf{C}^4\), состояние трех кубитов – вектор в пространстве \(\mathbf{C}^8\), то есть состояние \(N\) кубитов описывается вектором размерности \(2^N\) в комплексном пространстве. Вероятности каждой из возможных битовых строк (\(0000...00\), \(0000...01\), \(0000...10\), и так далее) получаются по методу Шредингера, который мы обсуждали в конце прошлой лекции:

\[ \mathbf{P}(\vec{s}) = | \bra{\Psi}\ket{\vec{s}} |^2 \]

Нужно отсортировать наши битовые строки в лексикографическом порядке – и вероятность i-й битовой строки будет равна квадрату i-го элемента вектора \(\ket{\Psi}\).

Формально, многокубитные состояния описываются с помощью математического концепта так называемого тензорного произведения, которое в случае линейных операторов идентично произведению Кронекера, обозначаемого значком \(\otimes\). Так, если \(\ket{\Psi}_A \in \mathrm{H}_A\) и \(\ket{\Psi}_B \in \mathrm{H}_B\), то \(\ket{\Psi}_{AB} = \ket{\Psi}_A \otimes \ket{\Psi}_B \in \mathrm{H}_{AB} = \mathrm{H}_{A} \otimes \mathrm{H}_{B}\). О том, как элементы вектора \(\ket{\Psi}_{AB}\) выражаются через элементы векторов \(\ket{\Psi}_{A}\) и \(\ket{\Psi}_{B}\), можно прочитать на Википедии в статье “Произведение Кронекера”.

Многокубитные операторы#

Как мы уже обсуждали ранее, квантовые операторы должны переводить текущее состояние в новое в том же пространстве и сохранять нормировку, а еще должны быть обратимыми. Значит, оператор для состояния из \(N\) кубитов – это унитарная комплексная матрица размерности \(2^N \times 2^N\).

Конструирование многокубитных операторов#

Прежде чем мы начнем обсуждать двухкубитные операторы, рассмотрим ситуацию. Представим, что у нас есть состояние из двух кубитов и мы хотим подействовать на первый кубит оператором Адамара. Как же тогда нам написать такой двухкубитный оператор? Мы знаем, что действуем на первый кубит оператором, а что происходит со вторым кубитом? Ничего не происходит – и это эквивалентно тому, что мы действуем на второй кубит единичным оператором. А финальный оператор \(2^2 \times 2^2\) записывается через произведение Кронекера:

\[\begin{split} \hat{H} \otimes \hat{I} = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \otimes \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = \frac{1}{\sqrt{2}} \begin{bmatrix} \hat{I} & \hat{I} \\ \hat{I} & -\hat{I} \end{bmatrix} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 \end{bmatrix} \end{split}\]

Учитывая, что многокубитные состояния конструируются аналогичным образом через произведение Кронекера, мы можем убедиться в верности нашего вывода:

print(np.allclose(np.kron(h @ basis, basis), np.kron(h, identity_gate) @ np.kron(basis, basis)))

True

Наблюдаемые для многокубитных гейтов#

Аналогичным образом можно сконструировать и наблюдаемые. Например, если мы хотим измерять одновременно два спина по оси \(\mathbf{Z}\), то наблюдаемая будет выглядеть так:

\[\begin{split} \mathbf{ZZ} = \hat{\sigma^z} \otimes \hat{\sigma^z} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \end{split}\]
print(np.kron(basis, basis).conj().T @ np.kron(pauli_z, pauli_z) @ np.kron(basis, basis))

[[1.+0.j]]

Основные двухкубитные гейты#

Основные многокубитные гейты, которые предоставляют современные квантовые компьютеры, – это двухкубитные гейты.

CNOT (CX)#

Квантовый гейт контролируемого инвертирования – это гейт, который действует на два кубита: рабочий и контрольный. В зависимости от того, имеет ли контрольный кубит значение 1 или 0, этот гейт инвертирует или не инвертирует рабочий кубит.

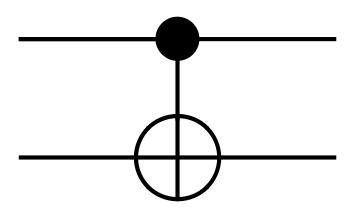
../../../_images/CNOT_gate.png

Fig. 24 Гейт CNOT#

Иногда этот гейт также называют гейтом CX. В матричном виде этот оператор можно записать так:

\[\begin{split} \hat{CNOT} = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0 \end{bmatrix} \end{split}\]
cnot = (1 + 0j) * np.array(
    [
        [1, 0, 0, 0],
        [0, 1, 0, 0],
        [0, 0, 0, 1],
        [0, 0, 1, 0],
    ]
)

print(np.allclose(cnot @ np.kron(basis, basis), np.kron(basis, basis)))
print(np.allclose(
    cnot @ np.kron(pauli_x @ basis, basis), np.kron(pauli_x @ basis, pauli_x @ basis)
))

True
True

Заметьте, тут мы воспользовались тем, что \(\hat{\sigma^x}\) работает так же, как инвертор кубитов: он превращает \(\ket{0}\) в \(\ket{1}\) и наоборот.

Гейты CY и CZ#

Схожие по принципу гейты – это гейты \(\hat{CY}\) и \(\hat{CZ}\). В зависимости от значения управляющего кубита к рабочему кубиту применяют соответствующий оператор Паули:

\[\begin{split} \hat{CY} = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & -i\\ 0 & 0 & i & 0 \end{bmatrix} \qquad \hat{CZ} = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & -1 \end{bmatrix} \end{split}\]

Гейт iSWAP#

Гейты \(\hat{CX}\), \(\hat{CY}\) и \(\hat{CZ}\) эквивалентны с точностью до однокубитных гейтов. Это означает, что любой из них можно получить, добавив необходимые однокубитные гейты до и после другого гейта. Например:

\[ \hat{CZ} = \left(\hat{I}\times\hat{H}\right)\hat{CX}\left(\hat{I}\times\hat{H}\right). \]

Этим свойством обладают отнюдь не все двухкубитные гейты. Например, таковым является гейт iSWAP:

\[\begin{split} \mathrm{iSWAP} = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & i & 0\\ 0 & i & 0 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \end{split}\]

Гейт fSim#

Для разных архитектур квантовых процессоров “естественный” гейт может выглядеть по-разному. Например, в квантовом процессоре Google Sycamore естественным является так называемый fermionic simulation gate или fSim. Это двухпараметрическое семейство гейтов вида:

\[\begin{split} \mathrm{fSim}(\theta, \phi) = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & \cos\theta & -i\sin\theta & 0\\ 0 & -i\sin\theta & \cos\theta & 0\\ 0 & 0 & 0 & e^{-i\phi} \end{bmatrix}. \end{split}\]

Впрочем, и fSim-гейт не является эквивалентным всему множеству двухкубитных гейтов. В общем случае, чем больше кубитов, тем сложнее будет выглядеть декомпозиция произвольного гейта на физически реализуемые в “железе”.

Первое знакомство с PennyLane#

На сегодняшний день существует достаточно много фреймворков для программирования квантовых компьютеров. Для целей этого курса мы будем использовать PennyLane. Эта библиотека предоставляет высокоуровневый Python API и создана специально для решения задач квантового машинного обучения.

import pennylane as qml

/home/runner/work/qmlcourse/qmlcourse/.venv/lib/python3.8/site-packages/_distutils_hack/__init__.py:33: UserWarning: Setuptools is replacing distutils.
  warnings.warn("Setuptools is replacing distutils.")

Device#

Для объявления квантового устройства используется класс Device. PennyLane поддерживает работу с большинством существующих квантовых компьютеров, но для целей курса мы будем запускать все наши программы лишь на самом простом симуляторе идеального квантового компьютера:

Note

Разработка и отладка квантовых алгоритмов, как правило, происходит на симуляторах. Но надо понимать, что это работает только пока алгоритмы – “игрушечные” и задействуют пару-тройку или пару десятков кубитов. Надо понимать, что при добавлении каждого следующего кубита требуется вдвое больше ресурсов, чтобы просимулировать квантовый компьютер. Поэтому симуляторы –принципиально плохо масштабируемые аналоги реальных квантовых компьютеров.

device = qml.device("default.qubit", 2)

Первый аргумент тут – указание устройства, а второй – число кубитов.

QNode#

Основной строительный блок в PennyLane – это qnode. Это функция, которая отмечена специальным декоратором и включает в себя несколько операций с кубитами. Результатом такой функции всегда является измерение. Напишем функцию, которая поворачивает первый кубит на \(45^o\), после чего измеряет оба кубита по оси \(\mathbf{Z}\).

Сначала на NumPy#

state = np.kron(basis, basis)
op = np.kron(ry(np.eye(2), np.deg2rad(45)), np.eye(2, dtype=np.complex128))
measure = np.kron(pauli_z, pauli_z)

print((op @ state).conj().T @ measure @ (op @ state))

[[0.70710678+0.j]]

Теперь через QNode#

@qml.qnode(device)
def test(angle):
    qml.RY(angle, wires=0)
    return qml.expval(qml.PauliZ(0) @ qml.PauliZ(1))


print(test(np.deg2rad(45)))

0.7071067811865472

Заключение#

Это последняя вводная лекция, где мы сами писали операторы и операции на чистом NumPy: это должно помочь лучше понять ту математику, которая лежит “под капотом” у квантовых вычислений. Дальше мы будем пользоваться только PennyLane и в отдельной лекции расскажем, как работать с этим фреймворком.

Итого:

  • мы знаем, что такое кубит;

  • понимаем линейную алгебру, которая описывает квантовые вычисления;

  • понимаем, как можно сконструировать нужный нам оператор и как его применить;

  • знаем, что такое измерение и наблюдаемые.

Теперь мы готовы к тому, чтобы знакомиться с квантовыми вариационными схемами и переходить непосредственно к построению моделей квантового машинного обучения.

Задачи#

  • Как связаны ось и угол вращения на сфере Блоха с собственными значениями и собственными векторами матрицы однокубитного гейта? Для этого найдите собственные векторы и собственные значения гейта \(R^\vec{n}\left(\alpha\right)\).

  • Вокруг какой оси и на какой угол вращает состояние гейт Адамара?

  • Гейт SWAP меняет кубиты местами. Его унитарная матрица имеет вид:

\[\begin{split} \mathrm{SWAP} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}. \end{split}\]

Попробуйте составить последовательность гейтов, реализующую \(\mathrm{SWAP}\), из гейтов \(\mathrm{iSWAP}\), \(\hat{CZ}\) и \(\hat{RZ}(\phi)\).