Формулировка задач оптимизации в терминах модели Изинга#

Автор(ы):

Не зря мы так глубоко изучали модель Изинга и анализировали ее решения – сегодня увидим, как в терминах этой модели можно сформулировать большинство важных задач комбинаторной оптимизации.

QUBO матрица#

Но сначала кратко обсудим так называемую QUBO матрицу [GKD19] – это еще один способ записать задачу модели Изинга, и дальше по курсу иногда будем этим пользоваться.

QUBO – это сокращение от Quadratic Unconstrained Binary Optimization, или, если переводить, то это задача квадратичной оптимизации без ограничений. То есть это такие задачи, для которых нет отдельных ограничений, например, равенств или неравенств, а функция стоимости представима в виде многочлена второй степени от входных переменных. Решением такой задачи является бинарный вектор \(X = \{x_1, x_2, ..., x_n\}\) такой, что \(x_1, ..., x_n \in \{0, 1\}\). В этом случае функцию стоимости \(C\) можно записать в виде:

\[ C = a_1 x_1^2 + a_2 x_2^2 + ... + a_n x_n^2 + b_1 x_1 + ... + b_n x_n + c_{1, 2} x_1 x_2 + c_{1, 3} x_1 x_3 + ... + c_{n, n - 1} x_n x_{n -1} \]

Но так как переменные бинарные, то разницы между \(x_i^2\) и \(x_i\) нет – дальше будем использовать \(a_i\) как единственные коэффициенты, считая, что \(b_i\) уже и так включены в \(a_i\). В этом случае можно представить функцию стоимости как матрицу размера \(|X| \times |X|\), на диагонали которой стоят коэффициенты \(a_1, ..., a_n\), а вне диагонали стоят коэффициенты, с которыми в стоимость входят пары элементов:

\[\begin{split} Q = \begin{pmatrix} a_1 & c_{1, 2} & ... & c_{1, n} \\ ... & ... & ... & ...\\ c_{n, 1} & ... & ... & a_{n} \end{pmatrix} \end{split}\]

Сама оптимизационная задача в этом случае формулируется следующим образом:

\[ \arg\min_{X} {X^T Q X} \]

Note

Тут рассматриваем именно минимизацию функции стоимости. Но если исходная задача формулировалась в терминах максимизации чего-то, например, как задача о рюкзаке или максимальном разрезе в графе, то очевидно, что просто домножив стоимость на -1, перейдем от максимизации к минимизации. Далее это будет важно, так как будем рассматривать задачу поиска основного состояния квантомеханической системы, а такое состояние – это по определению состояние именно с минимальной энергией.

QUBO как квантовый гамильтониан#

Если вспомнить, как выглядит модель Изинга, то легко заметить, что там, как и в QUBO-проблемах, есть лишь члены первой и второй степени. Вот только спиновые операторы (матрицы Паули) имеют собственные значения \(\pm 1\), а не \(\{0, 1\}\), которые фигурируют в QUBO. Это проблема, так как квадраты этих значений не равны им самим. Но это легко можно исправить введя “бинарный” оператор \(\hat{x}\):

\[\begin{split} \hat{x} = \frac{1 + \hat{\sigma}^z}{2} = \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} \end{split}\]

Введя “промежуточные” переменные \(sz_i\) которые связаны с \(x_i\) через это выражение (\(x_i = \frac{1 + sz}{2})\), всегда можно свести выражение для \(C\) к следующему виду:

\[ C = \sum_{i, j \in \{1, ..., |X|\}} J_{i, j} sz_i sz_j + \sum_{i \in {\{1, ..., |X|\}}} h_i sz_i \]

А это уже почти модель Изинга! Заменяем \(sz\) на операторы \(\sigma^z\) и получаем гамильтониан системы. Причем такой, что минимум его энергии будет совпадать с минимальным значением функции стоимости \(C\):

\[\begin{split} \begin{align*} & \hat{H} = \sum_{i, j \in \{1, ..., |X|\}} J_{i, j} \sigma^z_i \sigma^z_j + \sum_{i \in {\{1, ..., |X|\}}} h_i \sigma^z_i \\ & \braket{\Psi | \hat{H} | \Psi} = \min {X^T Q X} = \min {C,} \quad \text{если }\Psi\text{ -- это основное состояние системы} \end{align*} \end{split}\]

Причем в силу того, что у в выражении для \(\hat{H}\) фигурируют лишь \(\sigma^z\), основное состояние гамильтониана является “классическим”, то есть все спины “ориентированы” либо вверх, либо вниз, но не находятся в суперпозиции. Другими словами, гамильтониан диагонализируется в \(\mathbf{Z}\)-базисе.

Поиск основного состояния#

Как увидели, задачи, сформулированные в терминах QUBO, можно свести к задаче нахождения основного состояния квантовой системы, которая описывается некоторым оператором. Но что это вообще значит? И что это за гамильтониан такой, о котором все время говорим? Вообще говоря, гамильтониан – это оператор энергии:

\[ \hat{H} = \hat{T} + \hat{U}, \]

где \(T\) – это кинетическая энергия системы, а \(U\) – потенциальная энергия. Именно этот оператор определяет квантовую динамику в уравнении Шредингера. То есть это оператор, зная который (а также начальное состояние системы), можно посчитать волновую функцию системы (\(\ket{\Psi}(t)\)) в любой момент времени в будущем. Правда, это лишь в теории, так как сложность интегрирования уравнения Шредингера очень быстро растет с ростом размера системы. Этой темы немного уже касались в лекции про виды квантового машинного обучения, когда рассматривали, как нейросети помогают решать это самое уравнение.

Еще коснемся этой темы в следующих лекциях, но пока достаточно понимания того, что гамильтониан полностью описывает квантовую систему. С другой стороны, зная гамильтониан, всегда можем построить “в железе” квантовую систему, которую он описывает. Например, конфигурируя магнитные поля и двухчастичные обменные взаимодействия.

Таким образом, решение проблемы QUBO сводится к поиску \(\ket{\Psi}_{GS}\) – волновой функции, отвечающей основному состоянию:

\[ \arg\min_{\ket{\Psi}} {\hat{H}} \]

А финальное решение получается просто как наиболее вероятная конфигурация спинов в состоянии \(\ket{\Psi}_{GS}\). Ну и останется лишь перейти от полученных собственных значений операторов \(\sigma^z_i\) к собственным значениям операторов \(\hat{x}_i\).

Note

Кстати, справедлив и обратный переход, то есть решив проблему QUBO каким-нибудь из классических алгоритмов для решения комбинаторных задач, автоматически получим конфигурацию основного состояния соответствуеющей физической системы! Этот подход впервые был предложен аж в 1988-м году в работе [BGrotschelJungerR88]. Таким образом, приходим к пониманию тесной связи задач квантовой физики и комбинаторной оптимизации. Именно на этом и строится огромное число перспективных квантовых алгоритмов для решения задач реального мира. Особенно в NISQ эпоху!

Важное преимущество квантового представления QUBO-задач – в том, что наш мир устроен таким образом, что любая квантовая система всегда стремится в состояние с минимальной энергией, то есть основное. На этом построен даже целый класс квантовых аннилеров. Но и для вариационных квантовых алгоритмов это также дает свои преимущества.

Статья “Ising formulations of many NP problems”#

Основным источником информации для нас будет статья “Ising formulations of many NP problems” [Luc14], вышедшая в 2014-м году (версия 3). В данной лекции рассмотрим лишь часть примеров из этой работы, хотя наше рассмотрение будет чуть более подробным. В целом эта статья может быть использована как прекрасный справочник.

Задача о максимальном разрезе в графе (повторение)#

Уже рассматривали эту задачу в лекции о модели Изинга и в лекции про задачи комбинаторной оптимизации, но теперь повторим еще раз. Итак, есть граф на множестве вершин \(V\), связанных множеством ребер \(E\). Каждое ребро соединяет вершины \(u,v\). Для простоты будем рассматривать случай ненаправленного графа. Каждое ребро имеет вес \(w\). Цель – разбить множество вершин \(V\) на два непересекающихся сообщества \(V_1, V_2\) таким образом, чтобы суммарный вес ребер, соединяющих вершины из разных сообществ, был максимален:

\[ \arg\max{V_1, V_2} {\sum_{u,v,w \in E} w (\mathbf{1}(u \in V_1, v \in V_2) + \mathbf{1}(u \in V_2, v \in V_1))} \]
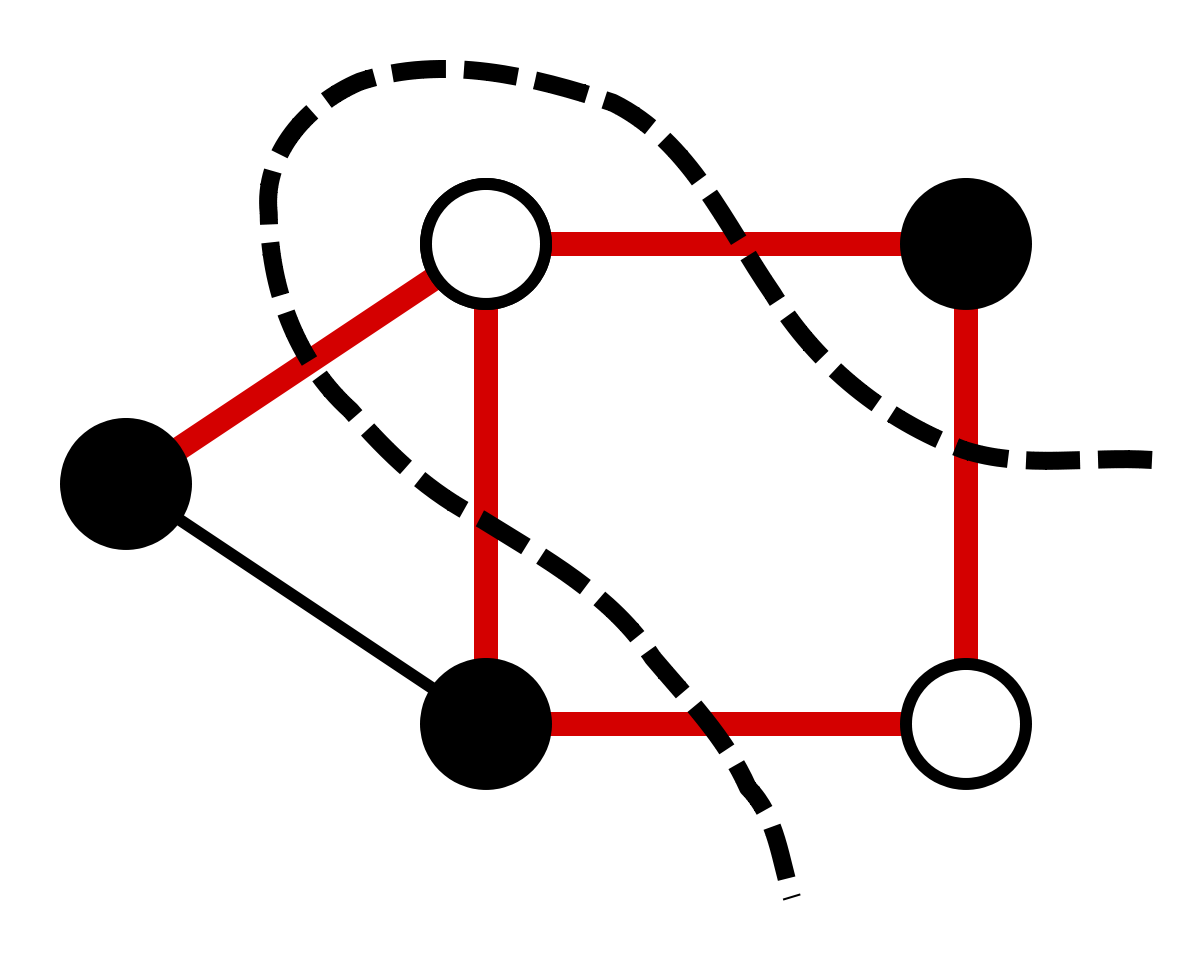
../../../_images/Max-cut.png

Fig. 93 Иллюстрация задачи о максимальном разрезе в графе#

Эта задача уже является задачей без ограничений и может быть сразу сформулирована в терминах QUBO и модели Изинга.

QUBO матрица#

QUBO матрица для этой задачи имеет размер \(|V| \times |V|\), а вектор решения \(X\) это, соответственно, будет бинарный вектор длины \(|V|\). Для простоты обозначим сообщество \(V_1\) как вершины, для которых \(x_i = 0\), а \(V_2\) это будут вершины с \(x_i = 1\). Еще хотим решать задачу минимизации вместо задачи максимизации. Запишем новую целевую функцию:

\[ C = - \sum_{i,j \in \{1, .., |V|\}} w_{i,j} (x_i + x_j - 2 x_i x_j) \]

Чтобы записать QUBO матрицу, будет удобнее работать с матрицей смежности графа, а не списком его ребер. Матрица смежности \(A\) (adjacency matrix) – это матрица размера \(|V| \times |V|\), элементы которой это веса \(w_{i, j}\), если в графе есть ребро между вершинами \(i\) и \(j\), и \(0\), если ребра нет. Тогда матрица QUBO будет иметь следующий вид:

\[\begin{split} QUBO = \begin{pmatrix} \sum_{j = 0}^{|V| - 1} A_{0,j} & -2 A_{0, 1} & ... & -2 A_{0, |V|} \\ ... & ... & ... & ... \\ -2 A_{|V|, 0} & ... & ... & \sum_{j = 0}^{|V| - 1} A{|V|, j} \end{pmatrix} \end{split}\]

Гамильтониан Изинга#

В случае этой задачи можно сказать, что она изначально имеет вид модели Изинга. И действительно, наиболее вероятная конфигурация спинов для основного состояния системы с гамильтонианом такого вида:

\[ \hat{H} = \sum_{i,j \in \{1, ..., |V|\}} (1 - \sigma^z_i \sigma^z_j) \]

будет в точности соответствовать решению задачи о максимальном разрезе. При этом численное значение энергии будет отличаться ровно на величину \(|E|\), то есть на число ребер, так как величина \((1 - \sigma^z_i \sigma^z_j)\) будет равна нулю, если вершины находятся в разных сообществах, или единице, если они находятся в одном.

Задача коммивояжера#

Задача коммивояжера обсуждалась в лекции по комбинаторной оптимизации, где были получены выражения для представления данной задачи в виде “без ограничений”. Напомним, что удалось добиться этого, “внеся” ограничения в выражения для целевой функции в виде штрафа за отклонение от ограничений. А также добавили соответствующие коэффициенты. Полученное в той лекции выражение имеет вид:

\[ C = A (1 - \sum_i x_{i,p})^2 + A (1 - \sum_p x_{i,p})^2 + A \sum_{u,v \notin E} x_{u,p} x_{v,p+1} + B \sum_{u,v,w \in E} w x_{u,p} x_{v,p+1} \]

Для нас удобно, что это уже задача минимизации. В данном случае QUBO-матрица получается при помощи явного раскрытия скобок в выражении для стоимости. Можно заметить, что в этом случае получаем также элементы 0-й степени, но формат QUBO-матрицы такого не предусматривает. Но во-первых, в данном случае легко можем определить разницу между \(X^T Q X\) и минимумом \(C\), а во-вторых, для нас это не столь важно – нам нужно решение, а значение энергии/функции стоимости получается без каких-либо проблем за полиномиальное время.

Note

Это довольно важное замечание, так как часто можно найти относительно простое представлениие задачи в виде QUBO, а вот учет всех констант может сильно усложнить ее вид. Более того, как увидим далее, не все представления QUBO одинаково эффективны, особенно когда переходят к решению на квантовом компьютере: для каких-то видов QUBO будет одна величина энергетической щели между основным и возбужденным состоянием в процессе решения, а для других QUBO-представлений той же задачи оно уже может стать больше!

Задача о выделении сообществ в графе#

Уже говорили об этой задаче в лекции про комбинаторную оптимизацию. Для этой задачи было разработано немало эвристических алгоритмов поиска [SCBR14], а в этой части сосредоточимся на формулировке как задачи QUBO.

\(k = 2\) сообществ#

В случае всего двух сообществ будем использовать двоичные спиновые переменные \(s_i \in \{-1,1\}\) для кодирования того, к какому именно сообществу принадлежит вершина \(i\). \(\frac{1 + s_is_j}{2}\) будет равняться \(1\), если \(i\) и \(j\) принадлежат одному сообществу, и \(0\) – в противном случае. Модулярность при этом будет следующей

(41)#\[\begin{split} M = \frac{1}{4m} s^T B s \\ \end{split}\]
(42)#\[ B_{ij} = (A_{ij} - \frac{g_i g_j}{2m}) \]

При \(s_i = 2 x_i - 1\) между спиновыми \(s_i \in \{-1,1\}\) и битовыми \(x_i \in \{0, 1\}\) переменными соответственно, а также \(\sum_{i,j} B_{i,j} = 0\), максимизация модулярности (42) может быть эквивалентна выражению задачи минимизации в форме QUBO с гамильтонианом \(H = - \frac{1}{m} x^T B x\) и с QUBO матрицей \(Q = - \frac{B}{m}\).

Множественные сообщества (\(k > 2\))#

Чтобы сформулировать задачу выделения \(k\) сообществ в канонической форме QUBO, сначала одновременно кодируем двоичные переменные \(x_i\), а затем строим QUBO-гамильтониан.

Используем схему однократного кодирования (one-hot encoding), в которой задаем \(x_{i,c} = 1\), если вершина \(i \in c\), и \(x_{i,c} = 0\) в противном случае, то есть,

(43)#\[\begin{split} x_{i,c} = \begin{cases} 1, если \ i \in c \\ 0, иначе \end{cases} \end{split}\]

Тогда потребуется \(k\) переменных на логическую вершину, и размер двоичного вектора решений \(x\) увеличится с вектора длины \(N\) для случая \(k = 2\) до \(k \times N\) для \(k\)-сообществ. В частности, задаем \(x = (x_{1,1}, x_{2,1}, ... , x_{N,1}, ... , x_{1,k}, x_{2,k}, ... , x_{N,k})\).

\(k > 2\) формулирует проблему как бинарную задачу минимизации, тогда возможно построить гамильтониан QUBO для \(k\)-сообществ с \(H_M = - \frac{1}{m} \sum_{c = 1}^k x_c^T B x_c\), в котором каждый член в сумме описывает бинарную задачу обнаружения сообщества для данного сообщества \(c\).

Представляя обобщенную матрицу модулярности \(Β\) размером \(kN \times kN\) и блочно-диагональной формы с \(B\) вдоль диагонали (44), можем переписать задачу обнаружения \(k\)-сообщества как задачу двоичной минимизации в каноническом формате QUBO (где исходные многоклассовые переменные вложены в большее число двоичных переменных):

\[ H_M = - \frac{1}{m} x^T B x \]
(44)#\[\begin{split} B = \begin{bmatrix} B & ... & 0 \\ \vdots & \ddots & \vdots \\ 0 & ... & B \end{bmatrix} \end{split}\]

Поскольку каждый узел \(i = 1, ... , N\) должен находиться ровно в одном сообществе \(c = 1, ... , k\), необходимо добавить штрафной член, чтобы ограничить решение для распределения сообществ. Формально это ограничение можно записать как \(\sum_{c = 1}^k x_{i,c} = 1\) при \(i = 1, ... , N\).

Это линейное ограничение можно добавить в задачу QUBO в виде квадратичного штрафного члена:

(45)#\[ H_P = P \sum_{i=1}^{N} (\sum_{c=1}^{k} x_{i,c} -1)^2 \]

с положительным предварительным коэффициентом \(P > 0\), обеспечивающим выполнение ограничений. Чтобы сформулировать штрафной член в (45) в QUBO-гамильтониан \(H_P = x^T Q_P x\), перенумеруем двоичный вектор решений, используя один подстрочный индекс от \(1\) до \(kN\), то есть \(x = (x_{1,1}, x_{2,1}, ... , x_{N,1}, ... , x_{N,k}) = (x_1, x_2, ... , x_N , ... , x_{kN} )\). Тогда штрафной член (45) может быть переписан как

(46)#\[ H_P = P (V x - b)^T (V x - b) \]

где \(b\) – вектор всех единиц, а \(V = [I_N, ... , I_N]\) – высокоструктурированная матрица размера \(N \times k_N\) с \(N \times N\) матрицами тождества, сложенными горизонтально рядом друг с другом. Если вес \(P\) достаточно велик, например, находится в диапазоне от \(1/N\) до \(10/N\), то штрафной гамильтониан \(H_P\) будет стремиться к решению, в котором все ограничения удовлетворены \(V_x = b\). Поскольку гамильтониан \(H_P\) квадратичен с точностью до константы, его можно переписать в канонической форме QUBO как \(H_P = x^T Q_P x\), с \(Q_P = P(V^TV - 2 \ \text{diag}(V^Tb))\).

Объединив модульности в уравнении (44) и штрафной гамильтониан в уравнении (46), получаем окончательный QUBO-гамильтониан для общего решения задачи о выделении \(k\) сообществ в графе

\[ H = H_M + H_p \]

Заключение#

Из этой лекции узнали, что такое QUBO матрица, а также как от такой формулировки оптимизационных задач можно перейти к задаче поиска основного состояния квантомеханической системы. В будущих лекциях познакомимся уже непосредственно с тремя основными методами решения этой задачи:

  1. квантовый отжиг В этом случае реализуем модель Изинга буквально в железе. Это сразу дает ряд ограничений и особенностей, но с другой стороны мы получаем возможность хорошо масштабировать систему. И действительно, сегодня компьютеры фирмы D-Wave имеют порядка нескольких тысяч кубитов. Многие специалисты считают, что до появления универсальных квантовых компьютеров именно аналоговые машины D-Wave, решающие задачу Изинга, станут основным коммерческим инструментов в квантовых вычислениях.

  2. вариационно-градиентные методы В этом подходе попытаемся закодировать волновую функцию основного состояния системы при помощи вариационной квантовой схемы, а дальше найти такие параметры, которые минимизируют результат измерения гамильтониана в таком состоянии. Этот метод называется Variational Quantum Eigensolver.

  3. третий популярный подход соединяет идеи первых двух В этом случае также делаем квантовый отжиг, но для этого не строим целевую систему в железе, а производим симуляцию квантовой динамики на кубитах при помощи специальных приближений из области квантовой механики. А параметры “отжига”, как и в VQE, подбираем при помощи градиентных методов. Такой подход носит название Quantum Approximate Optimization Algorithm.

Именно этим темам будет посвящена бОльшая часть оставшихся лекций.